 por DanielFerreira » Sex Fev 18, 2011 18:38
por DanielFerreira » Sex Fev 18, 2011 18:38
O valor da potência
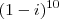
é:
a) - 32

b) 32

c) 16

d)

e) -

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Molina » Sex Fev 18, 2011 19:25
por Molina » Sex Fev 18, 2011 19:25
Olá.
Transforme o número para a representação trigonométrica:
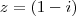
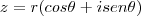
![z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)] z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)]](/latexrender/pictures/a2a0fdb7bb5363e545c297e7b9e43992.png)
Agora descubra o valor de

e

, posteriormente substituindo-os.
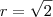
e
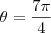
Caso tenha alguma dúvida de como obtê-los, avise. Depois basta substituir estes valores na equação, resolver as relações trigonométricas e chegar na resposta
a) -32i.
Bom estudo

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DanielFerreira » Ter Fev 22, 2011 16:26
por DanielFerreira » Ter Fev 22, 2011 16:26
Olá Molina,
também encontrei opção "a" como resposta, mas segundo o gabarito a resp. correta é "b"
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por Molina » Ter Fev 22, 2011 17:38
por Molina » Ter Fev 22, 2011 17:38
danjr5 escreveu:Olá Molina,
também encontrei opção "a" como resposta, mas segundo o gabarito a resp. correta é "b"
Boa tarde!
Muito estranho, pois:
![z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)] z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)]](/latexrender/pictures/a2a0fdb7bb5363e545c297e7b9e43992.png)
![z^{10}=(\sqrt{2})^{10}\left[cos\left(10 \frac{7 \pi}{4} \right) + i sen \left(10 \frac{7 \pi}{4}\right) \right] z^{10}=(\sqrt{2})^{10}\left[cos\left(10 \frac{7 \pi}{4} \right) + i sen \left(10 \frac{7 \pi}{4}\right) \right]](/latexrender/pictures/ecda6d8799ca8e342931a014430fc35b.png)
![z^{10}=32\left[cos\left(\frac{35 \pi}{2} \right) + i sen \left( \frac{35 \pi}{2}\right) \right] z^{10}=32\left[cos\left(\frac{35 \pi}{2} \right) + i sen \left( \frac{35 \pi}{2}\right) \right]](/latexrender/pictures/cbbc5b715fc63fd2ff61bbec68da3957.png)
![z^{10}=32\left[0 + i (-1) \right] z^{10}=32\left[0 + i (-1) \right]](/latexrender/pictures/f5026a614baa110e1322734e2cb5c745.png)
![z^{10}=32\left[-i \right] z^{10}=32\left[-i \right]](/latexrender/pictures/b5b2d78fd644b90a1e06f64bf4256a68.png)
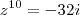 Resposta: a) -32i
Resposta: a) -32i.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por DanielFerreira » Qua Fev 23, 2011 15:28
por DanielFerreira » Qua Fev 23, 2011 15:28
De qualquer forma

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
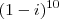 é:
é:





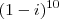 é:
é:





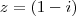
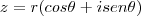
![z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)] z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)]](/latexrender/pictures/a2a0fdb7bb5363e545c297e7b9e43992.png)
 e
e  , posteriormente substituindo-os.
, posteriormente substituindo-os.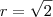
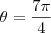



![z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)] z^{10}=r^{10}[cos(10 \theta ) + i sen(10 \theta)]](/latexrender/pictures/a2a0fdb7bb5363e545c297e7b9e43992.png)
![z^{10}=(\sqrt{2})^{10}\left[cos\left(10 \frac{7 \pi}{4} \right) + i sen \left(10 \frac{7 \pi}{4}\right) \right] z^{10}=(\sqrt{2})^{10}\left[cos\left(10 \frac{7 \pi}{4} \right) + i sen \left(10 \frac{7 \pi}{4}\right) \right]](/latexrender/pictures/ecda6d8799ca8e342931a014430fc35b.png)
![z^{10}=32\left[cos\left(\frac{35 \pi}{2} \right) + i sen \left( \frac{35 \pi}{2}\right) \right] z^{10}=32\left[cos\left(\frac{35 \pi}{2} \right) + i sen \left( \frac{35 \pi}{2}\right) \right]](/latexrender/pictures/cbbc5b715fc63fd2ff61bbec68da3957.png)
![z^{10}=32\left[0 + i (-1) \right] z^{10}=32\left[0 + i (-1) \right]](/latexrender/pictures/f5026a614baa110e1322734e2cb5c745.png)
![z^{10}=32\left[-i \right] z^{10}=32\left[-i \right]](/latexrender/pictures/b5b2d78fd644b90a1e06f64bf4256a68.png)
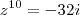




 .
.
 :
: