


Bem, não consigo me lembrar de como responder a este problema. Encontre o valor de k para o qual uma das raízes da equação x²-4kx+6k=0 é o quádruplo da outra. Alguém pode me ajudar? Grata
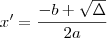
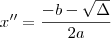
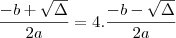

![- b + \sqrt{\Delta} = 4 . [- b - \sqrt{\Delta}] - b + \sqrt{\Delta} = 4 . [- b - \sqrt{\Delta}]](/latexrender/pictures/6fb7a2da2a5a364c61438a0c79f29caf.png)







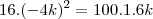
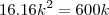


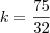

nainaneta escreveu:Bem, não consigo me lembrar de como responder a este problema. Encontre o valor de k para o qual uma das raízes da equaçãoé o quádruplo da outra. Alguém pode me ajudar? Grata
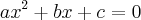 , é sabido que
, é sabido que 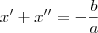 (soma das raízes) e
(soma das raízes) e 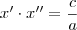 (produto das raízes).
(produto das raízes).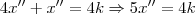


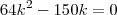
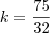 .
.

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: