 por shadowk » Qua Fev 16, 2011 19:09
por shadowk » Qua Fev 16, 2011 19:09
Boas!
Eu estou a tentar resolver um exame para me preparar melhor para o exame de recurso de sexta, só que tem uma questão que eu não estou mesmo a ver como se faz.
Recorrendo ao método de indução matemática, mostre que:
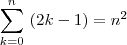
Agradeço a ajuda desde já.
-
shadowk
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Fev 16, 2011 18:58
- Formação Escolar: SUPLETIVO
- Área/Curso: informatica
- Andamento: cursando
 por Renato_RJ » Qua Fev 16, 2011 21:59
por Renato_RJ » Qua Fev 16, 2011 21:59
Boa noite amigo !! Tudo em paz ??
Seguinte, essa série é assim:

É fácil ver isso aplicando os valores de 0 e 1 no somatório, ao aplicarmos a indução para

teremos:
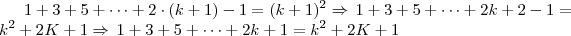
Só que

então, teremos:

Como os dois lados tem a mesma equação, está provado que a fórmula funciona para k+1.
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2680 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Indução Matemática
por gramata » Qua Set 02, 2009 16:52
- 0 Respostas
- 3063 Exibições
- Última mensagem por gramata

Qua Set 02, 2009 16:52
Problemas do Cotidiano
-
- Indução Matemática
por Abelardo » Qui Mar 31, 2011 03:04
- 1 Respostas
- 2529 Exibições
- Última mensagem por LuizAquino

Qui Mar 31, 2011 11:27
Álgebra Elementar
-
- Indução matemática
por TiagoFERD » Dom Mar 04, 2012 10:08
- 6 Respostas
- 4498 Exibições
- Última mensagem por TiagoFERD

Seg Mar 05, 2012 18:55
Progressões
-
- Indução Matemática
por MateusDantas1 » Dom Mar 04, 2012 13:00
- 1 Respostas
- 1722 Exibições
- Última mensagem por LuizAquino

Ter Mar 06, 2012 01:50
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
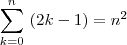

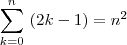


 teremos:
teremos: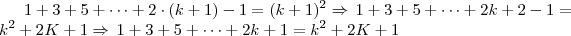
 então, teremos:
então, teremos:



 , avisa que eu resolvo.
, avisa que eu resolvo.

