 por Emilia » Qua Fev 16, 2011 12:06
por Emilia » Qua Fev 16, 2011 12:06
1. Uma pirâmide hexagonal regular tem aresta da base medindo 6cm. Se sua altura é de
10cm, qual será o comprimento de cada aresta lateral? Desenhe uma planificação para ela. (Você
pode usar o programa computacional Geogebra ou o Cabri Géomètre)
2. Um octaedro regular é seccionado na terça parte de suas arestas que concorrem em um
mesmo vértice e retiradas as pirâmides de base quadrada, resulta um poliedro arquimediano
composto por faces hexagonais regulares e faces quadradas chamado Octaedro truncado.
Dica: Procure descobrir se é possível usar a relação de Euler para achar o número de
vértices. Para o cálculo do número de diagonais, deduza uma expressão geral, partindo do
seguinte raciocínio: Considerando todos os vértices existentes no polígono, quantos
segmentos de retas podemos formar, sabendo que cada um destes segmentos é formado
por dois vértices? Deste número obtido, o que eu preciso retirar, para sobrar apenas as
diagonais do polígono?
a) Determine o número de vértices desse novo poliedro;
b) O número de diagonais desse novo poliedro;
c) determine a distância entre duas de suas faces quadradas opostas (paralelas). Para isto,
considere que, originalmente, cada aresta do octaedro regular media a cm.
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Renato_RJ » Qua Fev 16, 2011 12:31
por Renato_RJ » Qua Fev 16, 2011 12:31
Cara Emilia, tudo em paz ???
Seguinte, a primeira questão é bem tranquila, veja, se você tem uma piramide de base hexagonal regular, o ponto de encontro das arestas laterais terá projeção no centro da base, logo a distância entre um dos vértices do hexágono com o centro será 6 cm (lembre-se, o hexágono é regular), logo, use o teorema de Pitágoras (você verá um triângulo retângulo formado pela altura de 10 cm e a distância entre o vértice ao centro de 6 cm, a aresta lateral será a hipotenusa), e assim teremos uma aresta lateral de
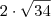
.
O segundo problema eu não entendi muito bem, vou tentar aqui....
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Emilia » Qua Fev 16, 2011 17:07
por Emilia » Qua Fev 16, 2011 17:07
Renato, obrigada pela ajuda.
No exercício 2 não consegui colocar a figura.
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Emilia » Qua Fev 16, 2011 17:09
por Emilia » Qua Fev 16, 2011 17:09
Renato, anexei um arquivo com a figura do ex. 2.
Obrigada.
- Anexos
-
[O anexo não pode ser exibido, pois a extensão doc foi desativada pelo administrador.]
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Renato_RJ » Qua Fev 16, 2011 18:24
por Renato_RJ » Qua Fev 16, 2011 18:24
Opa, com a figura melhorou sensivelmente, ainda mais levando em conta que geometria euclidiana não é a minha matéria favorita da matemática.. Desculpinha esfarrapada para os meus erros.. rsss...
Seguinte, o quê eu consegui fazer:
a) achei 24 vértices..
b)
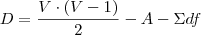
Mas eu contei com 8 faces hexagonais e 8 faces quadradas, para um octaedro truncado. Logo:
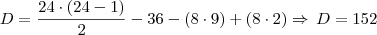
c) Se você considerar que a distância entre o centro do octaedro truncado até o centro da face hexagonal mede
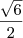
, então teremos:
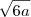
cm de distância entre as faces hexagonais passando pelo centro... A primeira fórmula é encontrada nos livros e até mesmo no site do Wolfram.
Quanto a formula de Euler, sim, ela pode ser usada, pois o sólido continua regular...
Antes de escrever tudo isso, dá uma conferida nas contas e definições, posso ter deixado passar algo...
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por Emilia » Qua Fev 16, 2011 23:26
por Emilia » Qua Fev 16, 2011 23:26
Renato, obrigada pela ajuda até agora!
Você viu que no ex. 1 pede para fazer a planificação da pirâmide? Pois é, já utilizei o winplot para construção de gráficos, agora o 'geogebra' nunca usei. Se você sabe como usar pode me passar o passo-a-passo de como construir a pirâmide?
Obrigada.
-
Emilia
- Usuário Ativo

-
- Mensagens: 22
- Registrado em: Ter Nov 30, 2010 15:19
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Renato_RJ » Qui Fev 17, 2011 01:11
por Renato_RJ » Qui Fev 17, 2011 01:11
Emilia, o que eu entendo por planificar uma pirâmide seria desenhar sua base... Mas, por via das dúvidas, segue um excelente canal do youtube que tem um tutorial do prof. Luiz Aquino (aqui do forum mesmo) -
http://www.youtube.com/user/LCMAquino - foi onde eu aprendi a usar o Geogebra...
[ ]'s
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por lucio Miranda » Qui Fev 17, 2011 13:50
por lucio Miranda » Qui Fev 17, 2011 13:50
Olá Renata , só pra retificar um dado na solucão do octaedro truncado: Ele tem 6 faces quadradas. Abraço
-
lucio Miranda
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Jan 31, 2011 12:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: formado
Voltar para Logaritmos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7323 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6037 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2871 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
-
- Geometria - help me?
por rybb » Ter Ago 25, 2009 07:55
- 3 Respostas
- 7315 Exibições
- Última mensagem por Molina

Qua Ago 26, 2009 23:18
Geometria
-
- geometria
por cristina » Qui Nov 19, 2009 07:05
- 0 Respostas
- 2466 Exibições
- Última mensagem por cristina

Qui Nov 19, 2009 07:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


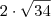 .
.
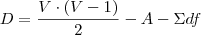
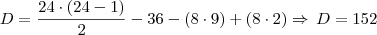
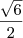 , então teremos:
, então teremos: 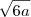 cm de distância entre as faces hexagonais passando pelo centro... A primeira fórmula é encontrada nos livros e até mesmo no site do Wolfram.
cm de distância entre as faces hexagonais passando pelo centro... A primeira fórmula é encontrada nos livros e até mesmo no site do Wolfram.