 por john » Ter Fev 15, 2011 15:37
por john » Ter Fev 15, 2011 15:37
Agora que já estou mais à vontade com as derivadas e com as integrias, parti para as derivadas parciais.

Mostre que:
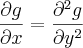
Se alguém perceber disto, que me dê uma ajuda. Já não me recordo desta matéria. Estou assistindo uns vídeos no Youtube que me estão a ajudar, mas este exercício não consegui resolver.
Cumprimentos!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Fev 15, 2011 16:18
por LuizAquino » Ter Fev 15, 2011 16:18
Seja a função real

.

: Essa notação significa que você deve derivar a função uma vez em relação a x, considerando que y é uma constante. Lembre-se que a derivada de uma constante é 0. Sendo assim, nós teremos:


: Essa notação significa que você deve derivar a função duas vezes em relação a y, considerando que x é uma constante.

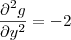
Portanto, vemos que

.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Ter Fev 15, 2011 16:30
por john » Ter Fev 15, 2011 16:30
Eu esqueci-me de pôr o sinal "-" antes de [/tex]\frac{\partial^2 g}{\partial y^2}[/tex]
O enunciado seria assim:

Logo seria verdadeiro certo?
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Ter Fev 15, 2011 16:40
por LuizAquino » Ter Fev 15, 2011 16:40
john escreveu:Eu esqueci-me de pôr o sinal "-" antes de

O enunciado seria assim:

Logo seria verdadeiro certo?
Sim.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Qua Fev 16, 2011 14:39
por john » Qua Fev 16, 2011 14:39
Ok. Obrigado!
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por john » Sáb Fev 19, 2011 14:29
por john » Sáb Fev 19, 2011 14:29

Neste exercício fiz a derivada pela regra do produto. Mas não me está dando igual. Dá-me 9 uma e 6 outra.
Alguém pode confirmar?
Obrigado.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Sáb Fev 19, 2011 14:38
por LuizAquino » Sáb Fev 19, 2011 14:38
Exercício: Seja
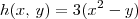
. Verifique que
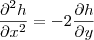
.
Derivando em relação a
x:

Derivando em relação a
y:
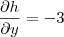
Portanto é válido que
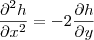
.
ObservaçãoSe estiver com dificuldades em entender as derivadas parciais acima, então procure enxergar a função como
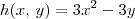
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por john » Sáb Fev 19, 2011 16:24
por john » Sáb Fev 19, 2011 16:24
Obrigado pela dica final. Fica mais fácil assim.
-
john
- Usuário Parceiro

-
- Mensagens: 50
- Registrado em: Sex Fev 11, 2011 22:46
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivadas parciais
por baianinha » Ter Jul 05, 2011 00:50
- 1 Respostas
- 2669 Exibições
- Última mensagem por MarceloFantini

Ter Jul 05, 2011 03:53
Cálculo: Limites, Derivadas e Integrais
-
- DERIVADAS PARCIAIS
por allyourwishes » Seg Jul 13, 2015 11:24
- 0 Respostas
- 2427 Exibições
- Última mensagem por allyourwishes

Seg Jul 13, 2015 11:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas parciais
por caarolsnp » Sex Out 13, 2017 11:40
- 0 Respostas
- 4331 Exibições
- Última mensagem por caarolsnp

Sex Out 13, 2017 11:40
Cálculo: Limites, Derivadas e Integrais
-
- [otimização] DERIVADAS PARCIAIS
por montanha » Seg Ago 04, 2008 10:18
- 5 Respostas
- 13092 Exibições
- Última mensagem por admin

Sex Ago 08, 2008 15:14
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Derivadas parciais
por -civil- » Qui Set 29, 2011 15:28
- 1 Respostas
- 2085 Exibições
- Última mensagem por LuizAquino

Sex Set 30, 2011 17:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

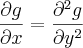


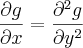

 .
. : Essa notação significa que você deve derivar a função uma vez em relação a x, considerando que y é uma constante. Lembre-se que a derivada de uma constante é 0. Sendo assim, nós teremos:
: Essa notação significa que você deve derivar a função uma vez em relação a x, considerando que y é uma constante. Lembre-se que a derivada de uma constante é 0. Sendo assim, nós teremos:
 : Essa notação significa que você deve derivar a função duas vezes em relação a y, considerando que x é uma constante.
: Essa notação significa que você deve derivar a função duas vezes em relação a y, considerando que x é uma constante.
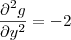
 .
.






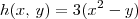 . Verifique que
. Verifique que 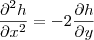 .
.
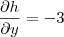
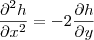 .
.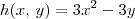 .
.



 , avisa que eu resolvo.
, avisa que eu resolvo.

