 por jeovani » Seg Fev 14, 2011 21:54
por jeovani » Seg Fev 14, 2011 21:54
olá nao estou conseguindo resolver esse exercicio, alguem do forum poderia me ajudar a chegar no resultado dessa questão ?
O MMC de 2 números naturais A e B é 1260.
Quando dividimos esse MMC por A e B o produto dos quocientes será igual a 90.
Ache A e B que satisfaçam está condição
A unica dica q tenho é essa abaixo
1260/a . 1260/b = 90
tentei fazer 1260.1260/90 = ab dando 17640 = ab fatorando da 2³.3².5.7² mais nao cheguei em nenhum resultado para achar a e b, alguem pode me ajudar aonde estou errando ?
Já tentei de tudo, quebrei a cabeça, não consegui resolver :/ alguem pode me ajudar por favor?
-
jeovani
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 14, 2011 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas / Sistemas de Informação
- Andamento: cursando
 por Molina » Seg Fev 14, 2011 22:33
por Molina » Seg Fev 14, 2011 22:33
Boa noite, Jeovani.
Temos duas informações do enunciado:
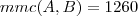
e
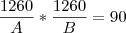
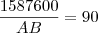

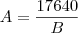
Logo, o que queremos descobrir é:

Milagrosamente, sendo
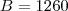
a conta fecha, veja:

Logo,

e
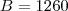
.
Perceba que
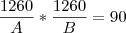
também é satisfeito.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por jeovani » Seg Fev 14, 2011 23:37
por jeovani » Seg Fev 14, 2011 23:37
entendii obrigado (y)

-
jeovani
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 14, 2011 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas / Sistemas de Informação
- Andamento: cursando
 por jeovani » Ter Fev 15, 2011 19:59
por jeovani » Ter Fev 15, 2011 19:59
nao entendi como chegou na resposta a = 14
-
jeovani
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 14, 2011 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas / Sistemas de Informação
- Andamento: cursando
 por Renks » Ter Fev 15, 2011 22:54
por Renks » Ter Fev 15, 2011 22:54
acho que posso lhe ajudar
SE , AB = 17640 e B = 1260
basta subtituir B na primeira equaçao ficando assim A . 1260 = 17640 entao A =
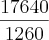
= 14
-
Renks
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Seg Fev 14, 2011 20:01
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por jeovani » Qui Fev 17, 2011 20:36
por jeovani » Qui Fev 17, 2011 20:36
o unico porem é que o "milagrosamente" nao pode entrar no meu calculo preciso de um raciocinio logico de por que estou usando o 1260. esse é o porém da questão, se alguem me da uma luz ae eu agradeço muito.
-
jeovani
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Seg Fev 14, 2011 21:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Exatas / Sistemas de Informação
- Andamento: cursando
 por LuizAquino » Qui Fev 17, 2011 23:20
por LuizAquino » Qui Fev 17, 2011 23:20
Temos que:

Além disso, temos que:

Sabemos que por definição o mmc entre dois números é o produto entre os fatores primos em comum (e com maior potência) e os que não estão em comum.
Analisando o mmc de A e B, podemos dizer que uma possível alternativa para A e B seria:
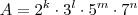
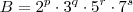
Por outro lado, analisando o produto entre A e B, temos que deve ocorrer:
k+p=3
l+q=2
m+r=1
n+s=2
Portanto, uma possibilidade para A e B seria:


Uma outra possibilidade para A e B seria:
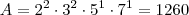
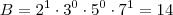
Mais outra possibilidade para A e B seria:

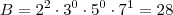
E ainda podemos achar outros pares A e B!
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- AJUDA NESTE EXERCÍCIO, POR FAVOR!
 por LVPM » Ter Nov 22, 2016 18:11
por LVPM » Ter Nov 22, 2016 18:11
- 2 Respostas
- 2306 Exibições
- Última mensagem por Cleyson007

Qua Nov 23, 2016 11:41
Funções
-
- [trigonometria] exercicio, me ajudem por favor?
por amanda s » Sex Nov 15, 2013 20:15
- 1 Respostas
- 7207 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 00:50
Trigonometria
-
- POR FAVOR ME AJUDEM NESTE EXERCÍCIO DE FATORAÇÃO
 por Claudia Sotero » Sáb Nov 21, 2009 22:09
por Claudia Sotero » Sáb Nov 21, 2009 22:09
- 4 Respostas
- 4876 Exibições
- Última mensagem por jonathan carvalho

Dom Nov 22, 2009 12:27
Cálculo: Limites, Derivadas e Integrais
-
- [exercicio de estatistica basica] URGENTE POR FAVOR
por ddesrosiers » Sex Dez 09, 2016 00:31
- 0 Respostas
- 7623 Exibições
- Última mensagem por ddesrosiers

Sex Dez 09, 2016 00:31
Estatística
-
- ajuda por favor
por zeramalho2004 » Dom Abr 05, 2009 21:31
- 3 Respostas
- 8658 Exibições
- Última mensagem por zeramalho2004

Seg Abr 06, 2009 10:25
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


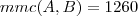
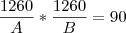
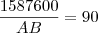

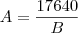

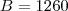 a conta fecha, veja:
a conta fecha, veja:
 e
e 

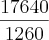 = 14
= 14

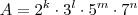
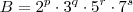


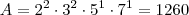
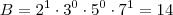

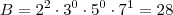
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
