A questão:
O número real x é tal que
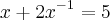 . Então, o valor de
. Então, o valor de 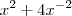 é:
é:No gabarito a resposta é: 21
Eu fiz arrumei ficou assim:
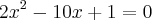
Meu delta deu 92, ai não consegui continuar. Se alguem puder ajudar agradeço.

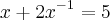 . Então, o valor de
. Então, o valor de 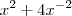 é:
é: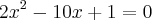

fernandocez escreveu:O número real x é tal que. Então, o valor de
é:
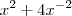 irá aparecer no primeiro membro.
irá aparecer no primeiro membro.


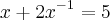 para obter a equação do 2° grau
para obter a equação do 2° grau  . Em seguida, substituir as soluções dessa equação na expressão
. Em seguida, substituir as soluções dessa equação na expressão 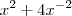 . A pessoa que escolher esse caminho verá que ele é bem mais longo do que a solução mais "elegante" apresentada acima. Além disso, é sempre bom lembrar que tempo é um fator crucial em concursos ou vestibulares.
. A pessoa que escolher esse caminho verá que ele é bem mais longo do que a solução mais "elegante" apresentada acima. Além disso, é sempre bom lembrar que tempo é um fator crucial em concursos ou vestibulares.

LuizAquino escreveu:
 , o valor de
, o valor de 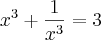
![{\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3} {\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3}](/latexrender/pictures/9914725c0448fa3d9b6df7e9a24a16e5.png) , elevei ao cubo ambos os membros e comecei a desenvolver.
, elevei ao cubo ambos os membros e comecei a desenvolver. = ...
= ... 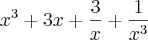

fernandocez escreveu:26) Se, o valor de
A resposta: 0
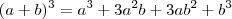 .
. .
.

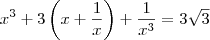



Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)