 por Iza » Ter Set 09, 2008 12:24
por Iza » Ter Set 09, 2008 12:24
Oi pessoal!.. Sou nova aqui, e não estou entendendo muito bem, como funciona isso aqui!


Preciso de ajuda! São 3 questões sobre geometria analítica - condição de três pontos. Perdi a aula de explicação e preciso apresentar elas hoje à noite!.. Alguém sabe resolver?!.. Tentei resolver com base nos exemplos porém não deu nada certo! São elas:
1. Dados os pontos A (1, 5) B (X, 3) e C (5, 0), o valor da abscissa de B para que os pontos sejam colineares é:
2. Determine o valor de A para que os pontos A (2, 1) B (a+1, 2) e C (-3, 1) :
a) Sejam colineares
b) Sejam os vértices de um triângulo
3. Os pontos A (-1, 3) B (2, 4) e C (-4, 10) são vértices de um triângulo. Determine a sua área.
Parece fácil, mas não to conseguindo fazer nenhuma!!!! Obrigada!
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Set 09, 2008 12:59
por Molina » Ter Set 09, 2008 12:59
Vou fazer a 1 para ver se a partir desta voce consegue fazer as outras:
1. Dados os pontos A (1, 5) B (X, 3) e C (5, 0), o valor da abscissa de B para que os pontos sejam colineares é: Primeiro de tudo é analisar a condição para que três pontos sejam colineares:
Três pontos quaisquer A, B, C serão colineares se o coeficiente angular de AB for igual ao coeficiente angular de BC.
Precisamos então ter que o coeficiente angular de AB seja igual ao coeficiente angular de BC.
Seja

o coeficiente angular:
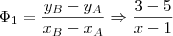
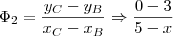
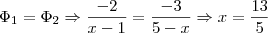
Fazendo um esboço do gráfico, você poe verificar que o resultado daria entre 2 e 3. E é o que ocorre, pois
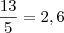
Tente fazer as outras da mesma forma.
Caso tenha dúvida, é só postá-la que alguem vai lhe ajudar.
Bom estudo!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Iza » Ter Set 09, 2008 16:52
por Iza » Ter Set 09, 2008 16:52
Muito obrigada Molina!.. Entendi direitinho! Valeu, mas vc me deixou os outros 2 abacaxis, que não consegui descascar! Olha só, começando pela n° 2 (não to saindo do chão), comecei fazendo como a questão n° 1 que você resolveu, olha no que deu!
YB - YA 2 - 1
----------- = -------------- E O QUE EU FAÇO AGORA, NÃO SEI CONTINUAR?
XB - XA a+1 - 2
YC - YB 1 - 2
---------- = -------------- E O QUE EU FAÇO AGORA, NÃO SEI CONTINUAR?
XC - XB -3 -(a+1)
ESTARIA ISSO MEIO CERTO?
essa é a letra a. (questão 2)
e a b. nem sei como começar pois pede: Sejam os vértices de um triângulo. Como de um triângulo??.. não tem nenhum exemplo em minha apostíla! :/
e o exercício 3, dá os pontostudo certinho, eu saberia fazer se fosse como a questão 1. Mas diz assim:
Os pontos A (-1,3) B (2, 4) E C (-4, 10) são vértices de um triângilo. Determine a sua área. Me ajudem!!!! Preciso isso pra hoje! Me de uma

Obrigada! ;/
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Set 09, 2008 18:25
por Molina » Ter Set 09, 2008 18:25
Iza, confirma as informações dos pontos do exercício 2.
Sao aqueles valores mesmo?
Aqui ta dando algo estranho...

Nao é dificil perceber que os pontos A e C formam uma linha horizontal com y = 1, pois seus y são igual a 1, e o ponto B já tem y = 2, ou seja, nunca o ponto B seria colinear aos outros dois pontos.
Acho que é isso...
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Iza » Ter Set 09, 2008 19:06
por Iza » Ter Set 09, 2008 19:06
Molina, são esses valores mesmo! Confirmo!! ;/
Mas quem sabe seja isso mesmo, não posso te dizer nada, porque não sei fazer, mas muito obrigada pela tentativa!
Beijos! Vou me arrumar e ir pra aula.. Hoje os 2 últimos períodos são matemática!!!!! Torce por mim! Ao menos tentei fazer! E vocês me ajudaram muito! heheh Valeu!
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Ter Set 09, 2008 19:14
por Molina » Ter Set 09, 2008 19:14
Espero que você se saia bem e depois comente aqui como foi.
Acho que no exercício 2) os pontos nao tem como ser colineares
(pelo motivo ja exposto a cima)
Ou seja, com isso concluimos que para qualquer qualquer a os três pontos não serão colineares. Com isso temos também que com três pontos não colineares é possível formar um triângulo (respondendo o item b).
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Ter Set 09, 2008 19:36
por admin » Ter Set 09, 2008 19:36
Olá.
Concordo com a conclusão. Outra forma de constatar, como comentei, é através de determinante, ou seja, devemos avaliar:
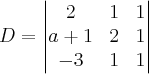
Se

, os pontos seriam colineares e poderíamos determinar

.
Como
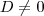
, os pontos não são colineares e necessariamente formam um triângulo.
A mesma idéia também pode ser aplicada no 1º exercício.
Para o 3º, podemos calcular a área

assim:
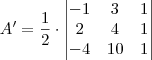
Bons estudos!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Iza » Qua Set 10, 2008 09:56
por Iza » Qua Set 10, 2008 09:56
Molina e Fábio, muito obrigada pela ajuda de vocês, me ajudaram e muuito mesmo!!!! (Pra quem perdeu a explicação em sala de aula, consegui entender com vocês e aposto que melhor do que se a professora me explicasse!.. No fim, olhem só Molina a questão 2 tinha um erro! Bem como você comentou que estava achando estranho e me pediu pra confirmar os dados (números) se eram esses mesmo, e eu a confirmei, porém chego no colégio e ninguém tinha conseguido fazer essa questão, pois era -1 ao invés de 1 aqui ó -> 2. Determine o valor de A para que os pontos A (2, 1) B (a+1, 2) e C (-3,
1) :
-1a) Sejam colineares
b) Sejam os vértices de um triângulo
A professora tinha se enganado! Que raivaaa!.. Aí como tinhamos 2 aulas, ela passou o teminha básico (umas 25 questões somente)

e deixou a última aula para começarmos o tema!.. Então re-fiz a questão 2, a 1 e a 3 acredito que estavam certinhas. Fiz a 3 no recreio, pois não tinha conseguido ver a resposta do Fábio (não tive como entrar aqui pois já era passado das 18:30) e estava me arrumando pra ir pra aula!................Entreguei as 3 questões, acho que todas estão certas, vamos ver! Agora pra amanhã tenho essas 25, só não sei como vou fazer, pois nem exemplos tem na apostíla! :// Qualquer coisa apareço por aqui!.. (Coisa bem provável) heheh.. Se conseguirem me ajudar novamente, beleza!! (Obs: vocês podem achar estranho, mas aqui tenho que entregar todas as questões de matemática, ela vai contar alguma coisa - nota).
Obrigada e até!! Bjss!
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Iza » Qua Set 10, 2008 17:39
por Iza » Qua Set 10, 2008 17:39
Pessoal! -----> Meu resultado: Até agora só me fecharam 3 questões apenas!!!!!.. To ferradaa!
01)Olhem só, começando pela 1 e não dando certo, fui pulando.. A questão 1 diz o seguinte -> Um ponto A pertence à bissetriz dos quadrantes ímpares e equidista de B (-2, -1) e C (7, 2). Determine as coordenadas do ponto A.
Aí começei assim, tentado usar essa fórmula (nem sei se é essa mesmo):
d AB = d AC ->
![\sqrt[ (XA - XC)2 + (YA - YB) 2]{} \sqrt[ (XA - XC)2 + (YA - YB) 2]{}](/latexrender/pictures/aa29170912a7baef9e71f5abfd208a2c.png)
-> equação dentro da raiz, é pra ser, e os 2s são ao quadrado.. porém não sei substituir! Porque eu não tenho o n° do A, justamente quero descobrir ele!!


(tem que dar (2, 2) )
02) Na questão 2, diz assim: No triângulo ABC, A(1, 1) é um dos vértices, G(3, 3) é o baricentro e M(3, 1) é o ponto médio do lado AB. Determine as coordenadas de B e C. Como é que eu determino? Não achei nenhuma fórmula! Não sei nem substituir mesmo se eu tiver a fórmula eu acho! Ajudem-me pleeease!
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por admin » Qua Set 10, 2008 17:47
por admin » Qua Set 10, 2008 17:47
Olá
Iza, boa tarde!
Como tentamos organizar os tópicos por assunto, para novas dúvidas, crie novos tópicos.
Estas mensagens do plantão são movidas posteriormente para a seção correspondente ao assunto e o título do tópico também é normalmente alterado para:
- Código: Selecionar todos
[assunto matemático] título escrito pelo usuário
Acumular vários problemas em um mesmo tópico dificulta a organização e buscas futuras dos visitantes.
Todo este seu tópico, por exemplo, provavelmente será movido para a seção de determinantes.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Iza » Qua Set 10, 2008 18:10
por Iza » Qua Set 10, 2008 18:10
Beleza!.. Desculpa, é que eu não sabia!.. Já passo pra outro! Obrigada!!
-
Iza
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Set 09, 2008 12:09
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- estou com uma duvida me ajudem ai!!
por weverton » Seg Jul 12, 2010 17:54
- 2 Respostas
- 2086 Exibições
- Última mensagem por weverton

Ter Jul 13, 2010 16:50
Estatística
-
- me ajudem estou com uma duvida
 por weverton » Qua Jul 28, 2010 17:59
por weverton » Qua Jul 28, 2010 17:59
- 1 Respostas
- 3686 Exibições
- Última mensagem por Lucio Carvalho

Qui Jul 29, 2010 07:44
Estatística
-
- estou com uma duvida me ajudem ai!!
por weverton » Qua Ago 04, 2010 17:05
- 2 Respostas
- 2262 Exibições
- Última mensagem por DanielRJ

Sex Ago 20, 2010 21:15
Estatística
-
- duvida de uma prova AJUDEM
por lais_banestes » Qua Mai 16, 2012 21:45
- 0 Respostas
- 1159 Exibições
- Última mensagem por lais_banestes

Qua Mai 16, 2012 21:45
Estatística
-
- Dúvida com Desvio Padrão! Ajudem me !
por Isa123 » Dom Dez 29, 2013 21:18
- 2 Respostas
- 4549 Exibições
- Última mensagem por Isa123

Qui Jan 02, 2014 11:18
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

 Preciso de ajuda! São 3 questões sobre geometria analítica - condição de três pontos. Perdi a aula de explicação e preciso apresentar elas hoje à noite!.. Alguém sabe resolver?!.. Tentei resolver com base nos exemplos porém não deu nada certo! São elas:
Preciso de ajuda! São 3 questões sobre geometria analítica - condição de três pontos. Perdi a aula de explicação e preciso apresentar elas hoje à noite!.. Alguém sabe resolver?!.. Tentei resolver com base nos exemplos porém não deu nada certo! São elas:

 o coeficiente angular:
o coeficiente angular: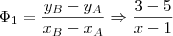
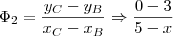
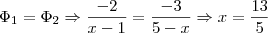
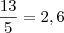



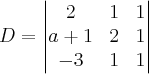
 , os pontos seriam colineares e poderíamos determinar
, os pontos seriam colineares e poderíamos determinar  .
.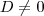 , os pontos não são colineares e necessariamente formam um triângulo.
, os pontos não são colineares e necessariamente formam um triângulo. assim:
assim: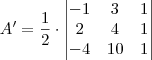

 e deixou a última aula para começarmos o tema!.. Então re-fiz a questão 2, a 1 e a 3 acredito que estavam certinhas. Fiz a 3 no recreio, pois não tinha conseguido ver a resposta do Fábio (não tive como entrar aqui pois já era passado das 18:30) e estava me arrumando pra ir pra aula!................Entreguei as 3 questões, acho que todas estão certas, vamos ver! Agora pra amanhã tenho essas 25, só não sei como vou fazer, pois nem exemplos tem na apostíla! :// Qualquer coisa apareço por aqui!.. (Coisa bem provável) heheh.. Se conseguirem me ajudar novamente, beleza!! (Obs: vocês podem achar estranho, mas aqui tenho que entregar todas as questões de matemática, ela vai contar alguma coisa - nota).
e deixou a última aula para começarmos o tema!.. Então re-fiz a questão 2, a 1 e a 3 acredito que estavam certinhas. Fiz a 3 no recreio, pois não tinha conseguido ver a resposta do Fábio (não tive como entrar aqui pois já era passado das 18:30) e estava me arrumando pra ir pra aula!................Entreguei as 3 questões, acho que todas estão certas, vamos ver! Agora pra amanhã tenho essas 25, só não sei como vou fazer, pois nem exemplos tem na apostíla! :// Qualquer coisa apareço por aqui!.. (Coisa bem provável) heheh.. Se conseguirem me ajudar novamente, beleza!! (Obs: vocês podem achar estranho, mas aqui tenho que entregar todas as questões de matemática, ela vai contar alguma coisa - nota). ![\sqrt[ (XA - XC)2 + (YA - YB) 2]{} \sqrt[ (XA - XC)2 + (YA - YB) 2]{}](/latexrender/pictures/aa29170912a7baef9e71f5abfd208a2c.png) -> equação dentro da raiz, é pra ser, e os 2s são ao quadrado.. porém não sei substituir! Porque eu não tenho o n° do A, justamente quero descobrir ele!!
-> equação dentro da raiz, é pra ser, e os 2s são ao quadrado.. porém não sei substituir! Porque eu não tenho o n° do A, justamente quero descobrir ele!!  } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: