 por jose henrique » Sáb Fev 12, 2011 20:35
por jose henrique » Sáb Fev 12, 2011 20:35
estou com uma questão que pede para provar que os números abaixos são irracionais.
![\sqrt[2]{2}+\sqrt[2]{3} \sqrt[2]{2}+\sqrt[2]{3}](/latexrender/pictures/621a970d954c080622ed136b68d1432b.png)
fiz de forma
![\sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5} \sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5}](/latexrender/pictures/91d9f158df3cdc029ab91b76399ee011.png)
![\sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2} \sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2}](/latexrender/pictures/9dfa21f7c9a4b6c0c4fd0f502b0dbd99.png)
bem então se b é um número natural múltiplo de 5 então a deverá ser míltiplo de 5.
até aí o meu racíocinio está correto.
obrigado pela ajuda
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Dan » Sáb Fev 12, 2011 21:07
por Dan » Sáb Fev 12, 2011 21:07
jose henrique, em primeiro lugar
![\sqrt[]{2}+\sqrt[]{3} \sqrt[]{2}+\sqrt[]{3}](/latexrender/pictures/8b216395c867c49551370f19db3878ed.png) não é
não é ![\sqrt[]{2+3} \sqrt[]{2+3}](/latexrender/pictures/e3cfe0476210e78ca6c5eaf3c150b6f0.png)
, muito menos
![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png)
. Você não pode sair somando raízes quadradas dessa forma, pois é como somar duas variáveis diferentes (x + y).
A ideia desse tipo de demonstração que você começou é da prova por absurdo. Você começa dizendo que uma raíz quadrada é igual a uma fração (o que já é um absurdo, já que essas raízes quadradas são irracionais) para no final constatar que se você seguir com esse processo algébrico obterá (daí sim) "o" absurdo (uma fração que pode ser simplificada para sempre, por exemplo).
Entendeu?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por jose henrique » Sáb Fev 12, 2011 21:18
por jose henrique » Sáb Fev 12, 2011 21:18
então eu terei que fazer este procedimento para cada raiz em questão, para depois que comprovadas que são números irracionais eu concluir que somando dois números irracionais o resultado será outro irracional.
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por jose henrique » Sáb Fev 12, 2011 21:27
por jose henrique » Sáb Fev 12, 2011 21:27
por exemplo nesta questão que pede Se i é um número irracional e n é um número inteiro então i + n é um número irracional.
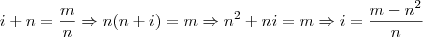
sendo que n

0
o que provaria, pois como i é irracional não poderia ser igualado a um racional e desta forma i + n seria racional
está correto?
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Dan » Sáb Fev 12, 2011 21:31
por Dan » Sáb Fev 12, 2011 21:31
Aí que mora o perigo. Não é correto afirmar que a soma de dois números irracionais é sempre irracional. No caso inicial será irracional, mas por exemplo,
![2 + \sqrt[]{2} 2 + \sqrt[]{2}](/latexrender/pictures/b949a09f0189582fd83e869b23343820.png)
e
![2 - \sqrt[]{2} 2 - \sqrt[]{2}](/latexrender/pictures/a125e0f784dea4fe3f49ff54aeac347c.png)
são dois números irracionais que quando somados dão 4. Então não dá pra generalizar.
Eu estou aqui pensando, e não consegui chegar a nenhuma estratégia. Provar que as raízes separadamente são irracionais é fácil, mas que argumento você vai usar no final para dizer que são irracionais?
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Dan » Sáb Fev 12, 2011 21:39
por Dan » Sáb Fev 12, 2011 21:39
Tudo bem, um inteiro somado com um irracional é irracional. Parece que você não concluiu essa outra demonstração, mas a afirmação está correta. Porém, isso ainda não resolve o problema da soma de dois irracionais.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Números Irracionais] Soma de irracionais dando um racional
por rnts » Seg Mai 21, 2012 16:15
- 1 Respostas
- 1699 Exibições
- Última mensagem por Guill

Sáb Mai 26, 2012 16:07
Álgebra Elementar
-
- Números irracionais
por cristina » Qua Set 16, 2009 23:40
- 1 Respostas
- 1962 Exibições
- Última mensagem por Marcampucio

Qui Set 17, 2009 00:18
Álgebra Elementar
-
- Números irracionais
por Marcia » Seg Nov 15, 2010 19:41
- 1 Respostas
- 1677 Exibições
- Última mensagem por Rogerio Murcila

Ter Nov 16, 2010 10:22
Álgebra Elementar
-
- Números irracionais
por lacesar » Dom Abr 12, 2015 16:52
- 1 Respostas
- 2188 Exibições
- Última mensagem por adauto martins

Ter Mai 08, 2018 18:41
Cálculo: Limites, Derivadas e Integrais
-
- Números irracionais
por lacesar » Dom Abr 12, 2015 16:59
- 1 Respostas
- 1174 Exibições
- Última mensagem por adauto martins

Sáb Abr 18, 2015 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[2]{2}+\sqrt[2]{3} \sqrt[2]{2}+\sqrt[2]{3}](/latexrender/pictures/621a970d954c080622ed136b68d1432b.png)
![\sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5} \sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5}](/latexrender/pictures/91d9f158df3cdc029ab91b76399ee011.png)
![\sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2} \sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2}](/latexrender/pictures/9dfa21f7c9a4b6c0c4fd0f502b0dbd99.png)

![\sqrt[2]{2}+\sqrt[2]{3} \sqrt[2]{2}+\sqrt[2]{3}](/latexrender/pictures/621a970d954c080622ed136b68d1432b.png)
![\sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5} \sqrt[]{2}+\sqrt[]{3}= \sqrt[]{3+2}= \sqrt[]{5}](/latexrender/pictures/91d9f158df3cdc029ab91b76399ee011.png)
![\sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2} \sqrt[]{5}=\frac{a}{b} \Rightarrow {\left(\sqrt[]{5} \right)}^{2}= {\left(\frac{a}{b} \right)}^{2} \Rightarrow 5 = \frac{{a}^{2}}{{b}^{2}}\Rightarrow5{b}^{2}={a}^{2}](/latexrender/pictures/9dfa21f7c9a4b6c0c4fd0f502b0dbd99.png)

![\sqrt[]{2}+\sqrt[]{3} \sqrt[]{2}+\sqrt[]{3}](/latexrender/pictures/8b216395c867c49551370f19db3878ed.png) não é
não é ![\sqrt[]{2+3} \sqrt[]{2+3}](/latexrender/pictures/e3cfe0476210e78ca6c5eaf3c150b6f0.png) , muito menos
, muito menos ![\sqrt[]{5} \sqrt[]{5}](/latexrender/pictures/0be1c4ad0f7708e4012e708b953ffd6c.png) . Você não pode sair somando raízes quadradas dessa forma, pois é como somar duas variáveis diferentes (x + y).
. Você não pode sair somando raízes quadradas dessa forma, pois é como somar duas variáveis diferentes (x + y).

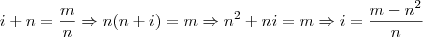
 0
0
![2 + \sqrt[]{2} 2 + \sqrt[]{2}](/latexrender/pictures/b949a09f0189582fd83e869b23343820.png) e
e ![2 - \sqrt[]{2} 2 - \sqrt[]{2}](/latexrender/pictures/a125e0f784dea4fe3f49ff54aeac347c.png) são dois números irracionais que quando somados dão 4. Então não dá pra generalizar.
são dois números irracionais que quando somados dão 4. Então não dá pra generalizar.






