Poliedros

por **Emilia** » Ter Fev 08, 2011 21:35

Preciso de ajuda com estes exercícios, não consegui o desenho do exercício 2.

1. Um poliedro convexo possui 2 faces hexagonais e 12 faces triangulares.
a) Determine o número de arestas desse poliedro.
b) Determine o número de vértices desse poliedro.

2 .a) Quantos planos existem passando pelo ponto médio de um segmento AB dado?
b) Quantos deles (dos planos que passam pelo ponto médio) são perpendiculares ao segmento?
c) A figura mostra representados o segmento AB e o plano alfa , passando pelo seu
ponto médio M. Que relação existe entre as distâncias entre esse plano e as
extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e
BB' ?

por **girl** » Sex Fev 11, 2011 10:45

1a)
2 hexágonos = 2.6lados=12 lados
12 triangulos = 12.3lados=36 lados
total 12+36 = 48 lados
Como cada dois lados determinam uma aresta, há 48/2 = 24 arestas

b)Utilize a "Relação de Euler": V - A +F = 2
V - 24 + (2+12) = 2
V = 24 -14+2
V = 12 vértice

por **LuizAquino** » Sáb Fev 12, 2011 11:38

Emilia escreveu:2 .a) Quantos planos existem passando pelo ponto médio de um segmento AB dado?
b) Quantos deles (dos planos que passam pelo ponto médio) são perpendiculares ao segmento?
c) A figura mostra representados o segmento AB e o plano alfa , passando pelo seu
ponto médio M. Que relação existe entre as distâncias entre esse plano e as
extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e
BB' ?

a) Dado um ponto qualquer, existem infinitos planos passando por ele.

b) Apenas um. Se o plano é perpendicular ao segmento, então o vetor diretor desse segmento corresponde a um vetor normal do plano. Além disso, o plano deve passar pelo ponto médio desse segmento. Dados um ponto (x0, y0, z0) e um vetor normal (a, b, c), determinamos apenas um plano, cuja equação é dada por a(x-x_0) + b(y-y_0) + c(x-z_0) = 0

.

c) Se o plano for perpendicular ao segmento, então os segmentos AA' e BB' sempre irão representar, respectivamente, a hipotenusa dos triângulos retângulos AMA' e BMB'. Nesse caso, aplicando o Teorema de Pitágoras em ambos os triângulos, obtemos que ${\overline{AA^{\prime}}}^2 - {\overline{BB^{\prime}}}^2 = {\overline{MA^{\prime}}}^2 - {\overline{MB^{\prime}}}^2$ . Já se o plano não for perpendicular ao segmento, não há muito o que afirmar.

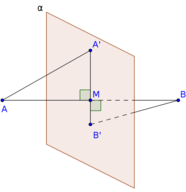
: Plano perpendicular a AB passando por seu ponto médio.; plano.png (9.24 KiB) Exibido 9133 vezes

Observação
Da próxima vez que a questão tiver uma figura, por favor poste-a também. Caso seja necessário, você pode criar suas figuras usando um programa como o GeoGebra. Para esse programa em particular, você pode encontrar um curso no meu canal no YouTube, cujo o endereço é:
http://www.youtube.com/LCMAquino

por **Emilia** » Sáb Fev 12, 2011 12:07

Luiz Aquino, muito obrigada.

Não coloquei a figura justamente por não saber como fazê-lo, mais uma vez agradeço a orientação.

por **LuizAquino** » Sáb Fev 12, 2011 13:25

Emilia escreveu:Não coloquei a figura justamente por não saber como fazê-lo

Não tem problema. Pelo menos agora você conhece uma opção para fazê-la!

Aliás, aproveito para dizer que, na minha opinião, é quase uma "obrigação" de qualquer Professor de Matemática atual dominar uma ferramenta como o GeoGebra. Por isso, comece a estudá-lo o quanto antes!

por **Lua** » Sáb Fev 12, 2011 19:13

Meu caro e querido colega, antes quero agradecer por tamanha generosidade .... olha esta figura é neste estilo, mas não nessa ordem. considerendo a mesma, vc modifica o angulo de 90° que fica A' e B' ( AA'M e BB'M ) as demais seguem, portanto a resposta muda??????????

Também estou no aguardo urgenteee da mesma.
Obrigada

por **Lua** » Sáb Fev 12, 2011 19:18

A figura mostra representados o segmento AB e o plano ? , passando pelo seu ponto médio M. Que relação existe entre as distâncias entre esse plano e as extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e BB' ?

Como se faz para inserir imagem aqui ?? pois fiz a figura mas num cola aqui

por **LuizAquino** » Dom Fev 13, 2011 00:07

Lua escreveu:(...) olha esta figura é neste estilo, mas não nessa ordem. considerendo a mesma, vc modifica o angulo de 90° que fica A' e B' ( AA'M e BB'M ) as demais seguem, portanto a resposta muda??????????

Sim. Obviamente a reposta muda.

De qualquer modo, considerando que A', M e B' são colineares como na figura anterior, o que irá alterar é que os triângulos AMA' e BMB' não serão mais retângulos. Ainda assim, os ângulos internos dos triângulos em M serão congruentes, já que por M temos que eles são opostos pelo vértice. O que podemos fazer é aplicar a Lei dos Cossenos:

$\overline{AA^\prime}^2 = \overline{MA}^2 + \overline{MA^\prime}^2 - 2\overline{MA}\; \overline{MA^\prime}\cos\beta$

$\overline{BB^\prime}^2 = \overline{MB}^2 + \overline{MB^\prime}^2 - 2\overline{MB}\; \overline{MB^\prime}\cos\beta$

A partir daí podemos manipular para obter alguma relação, lembrando que $\overline{MA} = \overline{MB} = \frac{\overline{AB}}{2}$ .

Lua escreveu:Como se faz para inserir imagem aqui ?? pois fiz a figura mas num cola aqui

Use a opção Anexar arquivo.

: Anexar.png (15.34 KiB) Exibido 8978 vezes

Em seguida, use o botão "Colocar na linha".

: Colar na linha.png (12.76 KiB) Exibido 8978 vezes

por **Lua** » Dom Fev 13, 2011 10:17

Caro amigo, acho q não me expressei direito na minha colocação sem imagem:
A figura mostra representados o segmento AB e o plano ? , passando pelo seu ponto médio M. Que relação existe entre as distâncias entre esse plano e as extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e BB' ?

A figura fica idem a postada por vc, mas modifica-se no angulo de 90° pois o angulo de 90° existe em AÂ'M e em BB'M
os triangulos são retangulos, pois os angulos A' e B' são de 90°,
ai vem a pergunta:
A figura mostra representados o segmento AB e o plano ? , passando pelo seu ponto médio M. Que relação existe entre as distâncias entre esse plano e as extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e BB' ?

Agora espero ter anexado a imagem corretamente pra vc ver.
Grata pelo carinhu e apoio.

por **Lua** » Dom Fev 13, 2011 10:23

Caro amigo eu consegui achar o item de anexar arquivo, ai eu procuro nos meus doc. e então fica dentro da caixinha ai so aparece oq esta na frente que é o item adicionar um arquivo, mas clicando la num anexa e esta outra opção q vc me auxiliou "colocar na linha" num sei onde se encontra e resumindo, num consigo anexar.
me orienta pois preciso dessa resposta ate amanha,,,,,,,,,, aiii!!!!!!

por **LuizAquino** » Dom Fev 13, 2011 16:43

Siga os passos para anexar uma imagem (ou qualquer outro arquivo):

Clique em "Anexar aquivo", como ilustra a primeira figura que enviei antes.
Clique no botão "Enviar arquivo...". Uma janela será aberta para que você possa selecionar um arquivo desejado. Após selecioná-lo, clique no botão "Adicionar um arquivo".
Após o envio ser processado, você verá abaixo de sua janela de edição a segunda figura que enviei antes. Agora, posicione o cursor no local do texto onde você quer que a imagem seja colocada. Em seguida, clique no botão "Colocar na linha". Você verá que na sua janela de edição irá aparecer na posição que você escolheu algo como:
Código: Selecionar todos
[attachment=1]imagem.png[/attachment]
Por fim, basta enviar a sua mensagem que automaticamente o código acima será substituído pela imagem desejada.

Lua escreveu:A figura fica idem a postada por vc, mas modifica-se no angulo de 90° pois o angulo de 90° existe em AÂ'M e em BB'M
os triangulos são retangulos, pois os angulos A' e B' são de 90°, ai vem a pergunta:
A figura mostra representados o segmento AB e o plano ? , passando pelo seu ponto médio M. Que relação existe entre as distâncias entre esse plano e as extremidades A e B, do segmento? Ou seja, que relação existe entre os segmentos AA' e BB' ?

Acredito que essa seja a figura.

: questao2.png (10.74 KiB) Exibido 8850 vezes

Agora, como dizia no Telecurso 2000: "vamos pensar um pouco..."

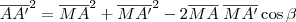
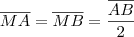Temos que $A\hat{M}A^\prime \equiv B\hat{M}B^\prime$ , pois esses ângulos são opostos pelo vértice. Temos também que $A\hat{A^\prime}M \equiv B\hat{B^\prime}M$ , pois os dois medem 90°. Por fim, sabemos que AM é igual a MB, pois M é ponto médio de AB. Conclusão: AA'M e BB'M são triângulos congruentes, pelo caso Lado-Ângulo-Ângulo Oposto. Logo, $\overline{AA^\prime} \equiv \overline{BB^\prime}$ .

Poliedros

Poliedros

Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Re: Poliedros

Quem está online