 por stanley tiago » Ter Fev 01, 2011 12:41
por stanley tiago » Ter Fev 01, 2011 12:41
a)

b)
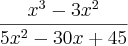
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por stanley tiago » Ter Fev 01, 2011 14:30
por stanley tiago » Ter Fev 01, 2011 14:30
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qua Fev 02, 2011 12:37
por DanielFerreira » Qua Fev 02, 2011 12:37
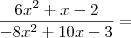
I) 6x^2 + x - 2
s = 1
p = - 12
6x^2 - 3x + 4x - 2 =
3x(2x - 1) + 2(2x - 1) =
(3x + 2)(2x - 1)II) - 8x^2 + 10x - 3
s = 10
p = 24
- 8x^2 + 4x + 6x - 3 =
- 4x(2x - 1) + 3(2x - 1) =
(2x - 1)(- 4x + 3)então,
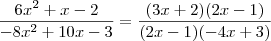
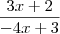
sua resp. está correta!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por DanielFerreira » Qua Fev 02, 2011 12:41
por DanielFerreira » Qua Fev 02, 2011 12:41
b)
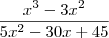
I) x³ - 3x² =
x²(x - 3)II) 5x² - 30x + 45 =
5(x² - 6x + 9) =
5(x - 3)²então,
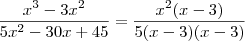
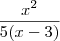
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por stanley tiago » Sex Fev 04, 2011 00:02
por stanley tiago » Sex Fev 04, 2011 00:02
obrigado , não sei o que seria de mim sem vcs

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qua Fev 09, 2011 12:56
por DanielFerreira » Qua Fev 09, 2011 12:56
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Simplifique as frações algébricas 02
por Ariel » Qua Set 28, 2016 21:21
- 0 Respostas
- 1616 Exibições
- Última mensagem por Ariel

Qua Set 28, 2016 21:21
Álgebra Elementar
-
- Simplifique as frações algébricas
por Ariel » Qui Set 29, 2016 13:52
- 0 Respostas
- 1304 Exibições
- Última mensagem por Ariel

Qui Set 29, 2016 13:52
Funções
-
- Fatoração: Simplifique as frações algébricas
 por Ariel » Dom Set 25, 2016 12:17
por Ariel » Dom Set 25, 2016 12:17
- 2 Respostas
- 2318 Exibições
- Última mensagem por Ariel

Sex Dez 09, 2016 00:26
Polinômios
-
- simplifique as expressões algébricas
por wattflix » Dom Out 04, 2015 17:12
- 1 Respostas
- 2041 Exibições
- Última mensagem por nakagumahissao

Dom Out 04, 2015 21:43
Polinômios
-
- frações algebricas
por tamirosa » Qui Out 29, 2009 20:11
- 1 Respostas
- 3308 Exibições
- Última mensagem por Molina

Sex Out 30, 2009 11:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

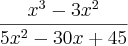


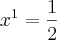
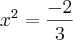



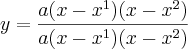
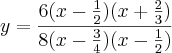
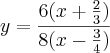
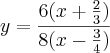 .
.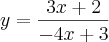

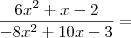
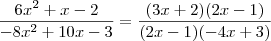
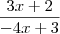

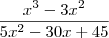
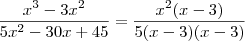
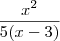






 .
.
 :
: