MAT0349
Regras do fórum
O objetivo desta seção é compartilhar alguns materiais dos próprios alunos do IME-USP, formandos e formados, das disciplinas do curso de Licenciatura em Matemática.
Dentre os materiais, organizados por disciplinas, você encontrará:
Provas aplicadas, notas de aulas, listas de exercícios, gabaritos e bibliografias, além de outros materiais indicados ou fornecidos pelos próprios professores.
A fonte e os créditos do autor devem ser citados sempre que disponíveis.
O intuito deste compartilhamento é favorecer um estudo complementar.
Utilize a seção de pedidos para outros ou caso a sub-seção ainda não possua material.
A pesquisa do fórum facilita a localização de materiais e outros assuntos já publicados.
 por Jaison Werner » Sáb Jan 29, 2011 10:58
por Jaison Werner » Sáb Jan 29, 2011 10:58
DETERMINE O VALOR LÓGICO ( V ou F ) DE CADA PROPOSIÇÕES:
UM TRIANGULO ESCALENO TEM TRES LADOS IGUAIS ? ( FALSO)
(a-b).(a+b)=

? (verdadeiro)
9 é divisivel por 3? (verdadeiro)
Quando a soma das medidas de dois ângulos é igual a 90º eles são ditos suplementares? (verdadeiro)
Uma piramide de base quadrada possui 4 vertices? (verdadeiro)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
é um numero irracional? (falso)
x=3 é a soluçao da equação 2x+6= 0?( falso)
Sen 90º = 1 ?(falso)
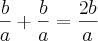
? (verdadeiro)
estão corretas?
-
Jaison Werner
- Usuário Parceiro

-
- Mensagens: 82
- Registrado em: Sex Abr 23, 2010 20:29
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em matematica
- Andamento: cursando
 por MarceloFantini » Sáb Jan 29, 2011 13:33
por MarceloFantini » Sáb Jan 29, 2011 13:33
Todas não.

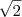
é irracional.
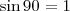
sim.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por VtinxD » Dom Jan 30, 2011 01:35
por VtinxD » Dom Jan 30, 2011 01:35
Só para completar, quando a soma é igual a 90° eles são ditos complementares
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por MarceloFantini » Dom Jan 30, 2011 01:41
por MarceloFantini » Dom Jan 30, 2011 01:41
Passou despercebido, obrigado Vtin.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Introdução à Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LOGICA DA MATEMATICA
por Jaison Werner » Sáb Jan 29, 2011 11:09
- 1 Respostas
- 8030 Exibições
- Última mensagem por Molina

Dom Jan 30, 2011 20:26
Introdução à Lógica
-
- Lógica da Matematica
por Jaison Werner » Qua Abr 27, 2011 12:19
- 6 Respostas
- 10884 Exibições
- Última mensagem por MarceloFantini

Qua Abr 27, 2011 21:31
Lógica e Conjuntos
-
- lógica matemática
por malbec » Ter Jun 02, 2015 11:25
- 1 Respostas
- 9536 Exibições
- Última mensagem por DanielFerreira

Dom Jun 07, 2015 12:38
Lógica
-
- Lógica Matemática URGENTE
por Jeffelim » Seg Fev 17, 2014 04:15
- 1 Respostas
- 3127 Exibições
- Última mensagem por Jeffelim

Seg Fev 17, 2014 13:04
Lógica
-
- lógica e matemática discreta
por ezidia51 » Seg Set 02, 2019 15:00
- 0 Respostas
- 13660 Exibições
- Última mensagem por ezidia51

Seg Set 02, 2019 15:00
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ? (verdadeiro)
? (verdadeiro)![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) é um numero irracional? (falso)
é um numero irracional? (falso)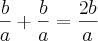 ? (verdadeiro)
? (verdadeiro)


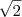 é irracional.
é irracional.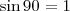 sim.
sim.
