 por stanley tiago » Dom Jan 23, 2011 12:19
por stanley tiago » Dom Jan 23, 2011 12:19
resolva esta equaçãe sujeitas a parâmetros , supostas possíveis em função dos seus coenficientes
A)
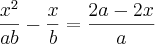
bom , a minha duvida é como encontrar a outra raiz dessa equaçao ,
já q tem tudas possíveis raizes pra esta equação !
eu vou postar como eu encontrei uma .
B)
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
essa eu nem consegui encontrar nenhuma raiz .
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por stanley tiago » Dom Jan 23, 2011 13:06
por stanley tiago » Dom Jan 23, 2011 13:06
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Jan 23, 2011 13:43
por Molina » Dom Jan 23, 2011 13:43
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por stanley tiago » Dom Jan 23, 2011 16:25
por stanley tiago » Dom Jan 23, 2011 16:25
entendi obrigado .
e enquanto a alternativa B) , como q fica ?
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Dom Jan 23, 2011 17:22
por Molina » Dom Jan 23, 2011 17:22
stanley tiago escreveu:entendi obrigado .
e enquanto a alternativa B) , como q fica ?
Boa tarde,
Você cometeu um erro fazendo
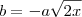
:
stanley tiago escreveu:B)
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2](/latexrender/pictures/d6ca2f3aa91588840034fdc4cc230beb.png)
O coeficiente não deveria ter o
x. Logo, o correto seria:
B)
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2](/latexrender/pictures/31482050f235b6ab4d711f86a6ec38e7.png)
Verifica se agora dá certo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por stanley tiago » Dom Jan 23, 2011 17:24
por stanley tiago » Dom Jan 23, 2011 17:24
ah entendi , obrigado

até mais
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- equações literais do 2° grau
por stanley tiago » Sáb Jan 22, 2011 12:16
- 5 Respostas
- 2848 Exibições
- Última mensagem por stanley tiago

Sáb Jan 22, 2011 16:19
Álgebra Elementar
-
- equações de 2º grau
por Lismara » Seg Ago 31, 2009 23:25
- 4 Respostas
- 2851 Exibições
- Última mensagem por Lismara

Ter Set 01, 2009 21:42
Sistemas de Equações
-
- Equações 2º Grau
por Quatroemes » Dom Mar 21, 2010 20:53
- 2 Respostas
- 2626 Exibições
- Última mensagem por Quatroemes

Seg Mar 22, 2010 11:34
Funções
-
- equacoes do 2 Grau
por guillcn » Qui Jun 30, 2011 12:30
- 1 Respostas
- 1602 Exibições
- Última mensagem por joaofonseca

Qui Jun 30, 2011 15:25
Equações
-
- equaçoes do 1 grau
por thalia alexandrina » Seg Out 10, 2011 14:29
- 3 Respostas
- 3015 Exibições
- Última mensagem por MarceloFantini

Ter Out 11, 2011 23:06
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
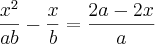
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)

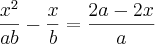
![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)

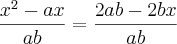
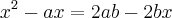

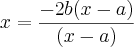

![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2x} ; c= -\frac{3}{2}a^2](/latexrender/pictures/d6ca2f3aa91588840034fdc4cc230beb.png)
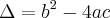
![\Delta=\left(-a\sqrt[]{2x} \right)^2-4.1.\frac{-3}{2}a^2 \Delta=\left(-a\sqrt[]{2x} \right)^2-4.1.\frac{-3}{2}a^2](/latexrender/pictures/c2dee4f5ab81e9da319eb5d6332d2c3a.png)
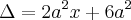
![\Delta=\sqrt[]{2a^2x+6a^2} \Delta=\sqrt[]{2a^2x+6a^2}](/latexrender/pictures/623101573d0d07144c9c1174404c01e7.png)
![\Delta=a^2\sqrt[]{2x+6} \Delta=a^2\sqrt[]{2x+6}](/latexrender/pictures/8303ab806ac0e74f0d65f389656a3881.png)
![\frac{-b+-\sqrt[]{\Delta}}{2a} \frac{-b+-\sqrt[]{\Delta}}{2a}](/latexrender/pictures/615dbc601d72ae78498ba5afd7ae9767.png)
![\rightarrow x^1=\frac{a\sqrt[]{2x}+a^2\sqrt[]{2x+6}}{2} \rightarrow x^1=\frac{a\sqrt[]{2x}+a^2\sqrt[]{2x+6}}{2}](/latexrender/pictures/d3b986dfb2b76180f8f24ba532b17af3.png)
![\rightarrow x^2=\frac{a\sqrt[]{2x}-(a^2\sqrt[]{2x+6})}{2} \rightarrow x^2=\frac{a\sqrt[]{2x}-(a^2\sqrt[]{2x+6})}{2}](/latexrender/pictures/2c80c30402dd4dd4a21c2d4e45a91243.png)

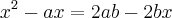


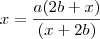




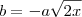 :
:![x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0 x^2-a \sqrt[]{2x}-\frac{3}{2} a^2=0](/latexrender/pictures/1edf18f82c9182d365ba679014b01163.png)
![a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2 a=1 ; b= -a\sqrt[]{2} ; c= -\frac{3}{2}a^2](/latexrender/pictures/31482050f235b6ab4d711f86a6ec38e7.png)





 .
.
 :
: