 por Renato_RJ » Seg Jan 17, 2011 10:41
por Renato_RJ » Seg Jan 17, 2011 10:41
Bom dia amigos !!!
Sei que aqui é a área de Álgebra elementar, mas não sei exatamente onde postar as minhas dúvidas em Álgebra abstrata, então resolvi criar o tópico aqui mesmo, qualquer problema por favor mudem o tópico de lugar.
Alguém poderia verificar se a demonstração que fiz está correta ?
Sejam

o Maior Divisor Comum deles.
Já que

é um ideal de

, então, pelo visto acima, existe

tal que

.
Mostre que

e portanto que existem
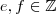
tais que

.
Desenvolvimento:Sendo

, temos:
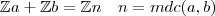
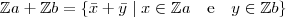
Agora tomemos um elemento

tal que
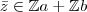
, então:
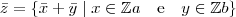
Então temos:
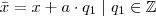
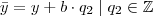
Logo:

![\bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] \bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/05fd58e774f06081f66fe3c1223043f5.png)
Onde
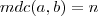
e

e chamaremos de

o termo
![[c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/81d5c6638da602680b5fa7fd694dfa2a.png)
.
Então teremos:
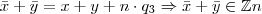

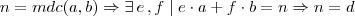
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Algebra abstrata
por iaslei » Ter Jul 05, 2011 00:01
- 2 Respostas
- 1372 Exibições
- Última mensagem por iaslei

Ter Jul 05, 2011 13:02
Álgebra Elementar
-
- Geometria Plana (abstrata)
por Celsoli » Seg Abr 12, 2010 12:10
- 0 Respostas
- 2221 Exibições
- Última mensagem por Celsoli

Seg Abr 12, 2010 12:10
Geometria Plana
-
- [algebra] ajuda
por santtus » Dom Fev 17, 2013 01:36
- 2 Respostas
- 1281 Exibições
- Última mensagem por santtus

Dom Fev 17, 2013 14:24
Aritmética
-
- algebra linear ajuda
por gutorocher » Sáb Set 18, 2010 22:36
- 3 Respostas
- 2167 Exibições
- Última mensagem por MarceloFantini

Seg Set 20, 2010 19:31
Álgebra Linear
-
- ajuda álgebra - funções f(x)
por joao henrique » Sex Jan 31, 2014 17:56
- 1 Respostas
- 891 Exibições
- Última mensagem por DanielFerreira

Sáb Fev 08, 2014 19:30
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 o Maior Divisor Comum deles.
o Maior Divisor Comum deles. é um ideal de
é um ideal de  , então, pelo visto acima, existe
, então, pelo visto acima, existe  tal que
tal que  .
.  e portanto que existem
e portanto que existem 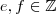 tais que
tais que  .
. , temos:
, temos: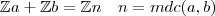
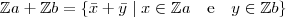
 tal que
tal que 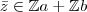 , então:
, então: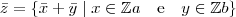
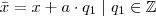
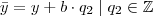

![\bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] \bar{x} + \bar{y} = x + y + mdc(a,b) \cdot [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/05fd58e774f06081f66fe3c1223043f5.png)
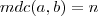 e
e  e chamaremos de
e chamaremos de  o termo
o termo ![[c_{1} \cdot q_{1} + c_{2} \cdot q_{2}] [c_{1} \cdot q_{1} + c_{2} \cdot q_{2}]](/latexrender/pictures/81d5c6638da602680b5fa7fd694dfa2a.png) .
.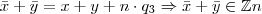

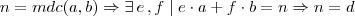


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.