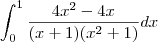 é : "
é : " Galera, tentei fazer essa integral por aquele método de divisao de polinomios ,e fazer A + B + C etc etc mas não deu certo nao ,alguem tem alguma idéia ?

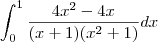 é : "
é : " 





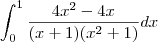
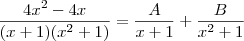
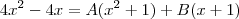
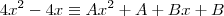
 e
e 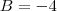
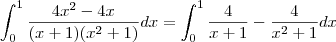
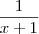 é
é  ; e a de
; e a de 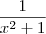 é
é 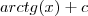 , temos (já substituindo os extremos de integração),
, temos (já substituindo os extremos de integração),![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)
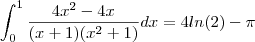

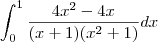
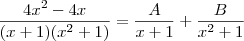
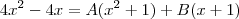
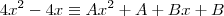
 e
e 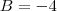
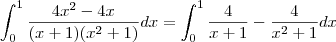
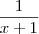 é
é  ; e a de
; e a de 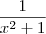 é
é 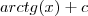 , temos (já substituindo os extremos de integração),
, temos (já substituindo os extremos de integração),![\int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)] \int_{0}^1 \frac {4}{x+1} - \frac{4}{x^2+1} dx = 4 [ln(2)-ln(1)] - 4[arctg(1)-arctg(0)]](/latexrender/pictures/98b5dd7dbc6c2cc0d1686e9a383a7925.png)
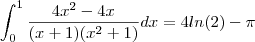

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)