 por NinhaH » Ter Jan 04, 2011 11:58
por NinhaH » Ter Jan 04, 2011 11:58
Oi pessoas... Bom dia!
Estou com problemas na resolução de exercicios sobre função composta... sei que para calcular uma fog(x) por exemplo devemos sustituir o x da f(x) pelo valor da f(g) ... mas... ainda tenho muitas dúvidas...
A questão é:
Se f (x) = x² - 2 e g (x) = 5x +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
, dê o domínio das funções e ache:
a) f o f (x)
b) g o g (x)
c) f o g (x)
d) g o f (x)
Eu estou resolvendo assim... Porém não sei se está correto.... Caso esteja errado me corrijam, por favor...
a) f o f (x)
= f (f (x))
(?2– 2)² - 2
?4 - 4 ?2 + 4 – 2
?4 - 4 ?2 + 2
b) g o g (x)
= g (g(x))
5 . (5 ? +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
) +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
25 ? + 5
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
+
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
25 ? + 6
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
c) f o g (x)
= f (g (x))
5 . (5 ? +
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
)² - 2
25 ? ² + 10 ?
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
+ ? - 2
25 ?² + 10 ? . ?1/2 + ? - 2
25 ?² + 10?3/2 + ? – 2
d) g o f (x)
= g (f (x))
5 . (?2– 2) +
![\sqrt[]{x^2-2} \sqrt[]{x^2-2}](/latexrender/pictures/edebf682d9dc1acefbbf1f490e7a913b.png)
5 ?² - 10 + (?2– 2)1/2
Obs: não consegui resolver esse calculo...
Agora a maior dúvida...
Como encontrar o dominio???
Me ajudem. por favor!!!
-
NinhaH
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Out 30, 2010 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Molina » Ter Jan 04, 2011 20:39
por Molina » Ter Jan 04, 2011 20:39
Boa noite.
Na letra b) você esqueceu de substituir o x que está dentro da raiz, veja:

Quanto ao domínio de funções, você terá que observar o "impedimento" que elas possuem, por exemplo:
Dada a função

. O

(domínio) não pode ser qualquer número, pois dentro da raiz só é possível valor
maior ou iguais a zero. Sendo assim, para eu descobrir o domínio desta função basta fazer:

Logo, o domínio da função f é:
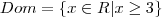
Qualquer dúvida, informe.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por NinhaH » Qui Jan 06, 2011 11:31
por NinhaH » Qui Jan 06, 2011 11:31
Verdade.... realmente esqueci de substituir o x da raiz....
Obrigada pela correção e pela explicação do calculo dos dominios....

-
NinhaH
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Out 30, 2010 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Funções Compostas.
por Sobreira » Sex Nov 16, 2012 16:27
- 9 Respostas
- 6336 Exibições
- Última mensagem por MarceloFantini

Sáb Nov 17, 2012 17:19
Funções
-
- calcular domínios de funções
por Regina » Qua Abr 06, 2011 21:17
- 4 Respostas
- 5839 Exibições
- Última mensagem por Regina

Dom Abr 10, 2011 12:38
Funções
-
- Desigualdades de funções compostas
por samra » Ter Fev 28, 2012 10:41
- 1 Respostas
- 1424 Exibições
- Última mensagem por LuizAquino

Ter Fev 28, 2012 15:54
Funções
-
- Concavidade de Funções Compostas
por danielfcastro » Seg Jun 10, 2013 20:05
- 0 Respostas
- 1128 Exibições
- Última mensagem por danielfcastro

Seg Jun 10, 2013 20:05
Funções
-
- Exemplos de reconhecimento de funções compostas.
por Sobreira » Seg Nov 26, 2012 14:25
- 1 Respostas
- 1647 Exibições
- Última mensagem por MarceloFantini

Seg Nov 26, 2012 19:05
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) , dê o domínio das funções e ache:
, dê o domínio das funções e ache:![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) ) +
) + ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) +
+ ![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) )² - 2
)² - 2![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png) + ? - 2
+ ? - 2![\sqrt[]{x^2-2} \sqrt[]{x^2-2}](/latexrender/pictures/edebf682d9dc1acefbbf1f490e7a913b.png)



 . O
. O  (domínio) não pode ser qualquer número, pois dentro da raiz só é possível valor
(domínio) não pode ser qualquer número, pois dentro da raiz só é possível valor 
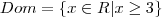


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  .
.
