 por DanielRJ » Ter Dez 28, 2010 19:30
por DanielRJ » Ter Dez 28, 2010 19:30
Olá vai anexo o seguinte triangulo onde o livro afirma um tal caso de semelhança ( LAL) , sendo que eu não consigo entender de onde ele faz tal afirmação então estou aqui
para obter ajuda. Bom a única coisa que consigo enxergar é que o angulo  é comum aos triângulos ABC e ADE.
 Editado a Base BC vale : X
Editado a Base BC vale : X
- Anexos
-
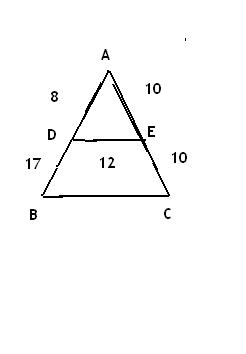
- semelhança.JPG (5.72 KiB) Exibido 5483 vezes
Editado pela última vez por
DanielRJ em Qua Dez 29, 2010 18:03, em um total de 1 vez.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Molina » Ter Dez 28, 2010 19:57
por Molina » Ter Dez 28, 2010 19:57
Boa noite, Daniel.
Perceba que DE é paralelo a BC, ou seja, o ângulo D é semelhante ao ângulo B. Da mesma forma o ângulo E é semelhante ao ângulo C.
Abraços!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Jefferson » Qua Dez 29, 2010 12:29
por Jefferson » Qua Dez 29, 2010 12:29
É impossível, resolver esse problema por semelhança de triângulos.
Veja AC/AE = 20/10 = 2.
AB/AD = 25/8.
O que elimina a possibilidade de DE ser paralelo a BC.
A solução pode ser obtida, aplicando o teorema dos cossenos no triângulo ADE.
achando o cosseno do ângulo A.
Com esse dado, aplico novamente o teorema dos cossenos no triângulo ABC.
Determino BC.
BC/DE terá outro valor. O que prova que os triângulos, nao sao semelhantes.
Duvidas, entre em contato.
jesufra@hotmail.comJefferson.
-
Jefferson
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Ter Nov 16, 2010 23:18
- Localização: Vila Velha - ES
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por 0 kelvin » Qua Dez 29, 2010 13:16
por 0 kelvin » Qua Dez 29, 2010 13:16
Esse triângulo esta errado. Se fosse um triângulo equilátero, já seria impossível, deveria acontecer DA = AE e DB = EC.
Se o segmento DE é tal que ele divide os lados do triângulo ABC do jeito que esta na figura, DE não pode ser paralelo a BC.
Dois lados são conhecidos e um ângulo notável, aí é lei dos cossenos.
Como os lados AB e AC não são iguais, se vc traçar uma altura da base BC até o vértice A, o ângulo de 60 não se divide em dois de 30. Então não tem como usar Pitágoras aí.
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por DanielRJ » Qua Dez 29, 2010 17:36
por DanielRJ » Qua Dez 29, 2010 17:36
o Enunciado não fala nada sobre DE//BC, se ele falasse eu saberia resolver o caso é que ele não cita nada.
Este exercicio é do livro fundamentos da matematica elementar.
vamos lá sendo DE//BC e angulo  comum aos 2 triangulos teremos um caso de semelhança:
Então colocando a Razão de semelhança em pratica teremos:
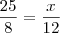
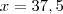
sendo que no livro a resposta é

.
Editado pela última vez por
DanielRJ em Qua Dez 29, 2010 17:59, em um total de 1 vez.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Qua Dez 29, 2010 17:55
por MarceloFantini » Qua Dez 29, 2010 17:55
Você tem o enunciado completo, ou desenho?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por 0 kelvin » Qua Dez 29, 2010 20:05
por 0 kelvin » Qua Dez 29, 2010 20:05
É uma questão que descreve o triângulo e não mostra o desenho?
Se o segmento DE é paralelo a BC e o segmento AC esta dividido em duas metades de 10 unidades, então estou vendo um trapézio e um triângulo, pois se 17 > 10, então o segmento que vale 17 não pode pertencer à mesma reta do segmento que vale 8.
Mas se DE não é paralelo a BC, então o segmento DE tem o ponto E no ponto médio de AC, mas o ponto D não esta no ponto médio de AB. Daí tem dois triângulos com um ângulo em comum, mas tem tambem um quadrilátero de 4 lados diferentes na figura. Nesse caso o ângulo comum não garante semelhança.
- Anexos
-
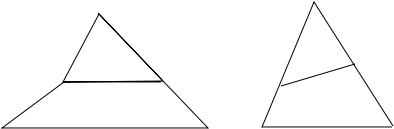
- triangulo.png (3.34 KiB) Exibido 5452 vezes
-
0 kelvin
- Usuário Parceiro

-
- Mensagens: 78
- Registrado em: Dom Out 31, 2010 16:53
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciencias atmosfericas
- Andamento: cursando
 por Otavio Rubiao » Qui Jan 27, 2011 10:36
por Otavio Rubiao » Qui Jan 27, 2011 10:36
Eu acho que a semelhança se dá não pelo fato dos lados serem congruentes mas sim por serem proporcionais....
Como o angulo A é igual nos dois triangulos e temos que 20/8 = 25/10 . Conseguimos estabelecer que a constante de semelhança entre os triangulos é 2,5 logo:
x/12 = 2,5 , x = 30.
espero ter ajudado...
qualquer coisa
Otavio__moura@hotmail.com
-
Otavio Rubiao
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Jan 27, 2011 10:24
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Plana
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Semelhança de triângulos] Triângulos quadrados
 por Debora Bruna » Seg Ago 08, 2016 12:18
por Debora Bruna » Seg Ago 08, 2016 12:18
- 0 Respostas
- 1473 Exibições
- Última mensagem por Debora Bruna

Seg Ago 08, 2016 12:18
Geometria Plana
-
- Semelhança de triângulos
 por igorcamilo » Sáb Jun 04, 2011 19:55
por igorcamilo » Sáb Jun 04, 2011 19:55
- 1 Respostas
- 2442 Exibições
- Última mensagem por Adriano Tavares

Dom Jan 01, 2012 14:55
Geometria Plana
-
- Semelhança de triângulos
por Gaussiano » Sáb Dez 10, 2011 13:59
- 0 Respostas
- 1587 Exibições
- Última mensagem por Gaussiano

Sáb Dez 10, 2011 13:59
Geometria Plana
-
- semelhanca de triangulos
por bmachado » Ter Mar 13, 2012 17:02
- 1 Respostas
- 1484 Exibições
- Última mensagem por bmachado

Ter Mar 13, 2012 17:20
Geometria Plana
-
- Semelhança de triângulos
por TAE » Qua Jun 20, 2012 01:12
- 2 Respostas
- 4440 Exibições
- Última mensagem por Russman

Qua Jun 20, 2012 05:01
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








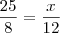
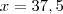
 .
.



