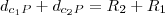por sorchilas » Sáb Dez 11, 2010 12:55
por sorchilas » Sáb Dez 11, 2010 12:55
Oi pessoal,
Sou novo no forum e sem grande experiência na área de matemática. Ultimamente me deparei com duas questões que não consigo nem "sair do canto". Espero que vocês possam me ajudar neste aspecto, visto que a probabilidade de uma destas ou as duas caírem na minha prova de Segunda-feira. Oo As questões estão nas imagens abaixo.
http://img522.imageshack.us/i/questo13.jpg/http://img20.imageshack.us/i/questo30.jpg/Por favor, me ajudem!
-
sorchilas
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Dez 11, 2010 12:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharias
- Andamento: cursando
 por VtinxD » Dom Dez 12, 2010 12:26
por VtinxD » Dom Dez 12, 2010 12:26
É raro ver questões boas como essas em provas.Mas vamos as tentativas de resolução.
Questão 30)Não sei se conhece as propriedades ópticas das elipses,mas vou tentar explica-las aki e se estiver errado por favor me corrijam.Desenhe uma elipse,agora desenhe sua tangente e que intercepta a elipse no ponto P.Tente se lembrar da sua aula de ótica onde a imagem de um objeto,no espelho plano, fica do outro lado do espelho e a distancia de qualquer ponto do espelho,tangente, ao objeto e igual a distancia à imagem.Utilizando disso com os focos e perceba oque acontece.
A outra não vou tentar porque estou sem tempo.
Espero ter ajudado
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por VtinxD » Dom Dez 12, 2010 14:09
por VtinxD » Dom Dez 12, 2010 14:09
*A questão 13 e mais complicada.Vou expor aqui a minha solucao:
Questão 13)Se pegar um ponto P

.Temos:

Provavelmente vai dar uma hiperbole porque se voce passar o
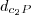
para o outro lado e o
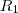
para o lado do

voce tera que a distancia de P aos centros e sempre uma constante que define uma hiperbole com foco nos centros das circunferencias.
Correcao:isso so vai ser verdade para pontos fora da circunferencia,para pontos dentro da circunferencia sera formada uma elipse.Pois a soma da distancia dos centros ao ponto sera constante.
*PS:O teclado que estou usando tem poucos acentos.
Espero ter ajudado pelo menos um pouco.
Editado pela última vez por
VtinxD em Dom Dez 12, 2010 15:06, em um total de 2 vezes.
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por sorchilas » Dom Dez 12, 2010 14:15
por sorchilas » Dom Dez 12, 2010 14:15
Oi Amigão,
Desde já agradeço a preocupação e ajuda! Agora a tarde estou indo assistir a uma aula( Aula no Domingo Ninguém merece!), quando voltar a noite, vou tentar arrumar forças para quebrar a cabeça com esses problemas... rsrs
Obrigado e Abraços
-
sorchilas
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Dez 11, 2010 12:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharias
- Andamento: cursando
 por andrefahl » Dom Dez 12, 2010 18:08
por andrefahl » Dom Dez 12, 2010 18:08
Ola,
na questão 13 vc tem duas elipses,
transladadas no eixo x.
faça x1 = (x-3)
dai vc vai perceber que se trata da equação d uma elipse
pois x^2/a + y^2/b = 1 essa é a eq d uma eplise.
lembra que a circ eh uma elipse com focos coincidentes =)
uma delas vc vai ter q dividir tudo por 81 pra ter no lado esquerdo 1 =D
att
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por andrefahl » Dom Dez 12, 2010 18:09
por andrefahl » Dom Dez 12, 2010 18:09
soh corrigindo pq esqueci.. o a e b na eq saum elevados ao quadrado =)
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por VtinxD » Dom Dez 12, 2010 18:41
por VtinxD » Dom Dez 12, 2010 18:41
São duas elipses mais uma hipérbole,certo?
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por andrefahl » Dom Dez 12, 2010 22:46
por andrefahl » Dom Dez 12, 2010 22:46
HASUdhauds a outra eu nem vi naum...
soh a primeira q saum duas elipses =)
-
andrefahl
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Qui Out 28, 2010 18:05
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física - UNICAMP
- Andamento: cursando
 por VtinxD » Dom Dez 12, 2010 23:09
por VtinxD » Dom Dez 12, 2010 23:09
Estava pensando e cheguei a uma conclusão e nela temos 3 casos:

1°Caso)

,teremos uma hipérbole pois os dois serão positivos ,pois:
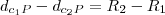
e como

é constante segue a definição de hipérbole.
2°Caso)
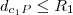
ou

.Teremos uma elipse e não importa qual vai ser menor os focos serão os mesmos e suas medidas também,pois:
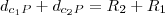
3ºCaso)tex]{d}_{{c}_{1}P}\leq{R}_{1}[/tex] e

.Teremos uma "seção" da hipérbole achada antes com mesmo foco e mesmas medidas,pois:
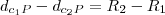
e como

é constante segue a definição de hipérbole.
É assim que vejo essa questão espero ter ajudado e se estiver errado então por favor me ensinem!
-
VtinxD
- Usuário Parceiro

-
- Mensagens: 64
- Registrado em: Dom Ago 15, 2010 18:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado em Matematica
- Andamento: cursando
 por sorchilas » Seg Dez 13, 2010 12:30
por sorchilas » Seg Dez 13, 2010 12:30
andrefahl escreveu:Ola,
na questão 13 vc tem duas elipses,
transladadas no eixo x.
faça x1 = (x-3)
dai vc vai perceber que se trata da equação d uma elipse
pois x^2/a + y^2/b = 1 essa é a eq d uma eplise.
lembra que a circ eh uma elipse com focos coincidentes =)
uma delas vc vai ter q dividir tudo por 81 pra ter no lado esquerdo 1 =D
att
Oi amigão,
Não entendi direito o que devo fazer... #) Como é que devo fazer mesmo?
Grato,
-
sorchilas
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Dez 11, 2010 12:45
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharias
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Cônicas e quádricas
 por Danilo » Ter Jan 08, 2013 13:25
por Danilo » Ter Jan 08, 2013 13:25
- 2 Respostas
- 5111 Exibições
- Última mensagem por Danilo

Qui Abr 04, 2013 00:43
Geometria Analítica
-
- Cônicas e quádricas
por Danilo » Ter Jan 08, 2013 13:27
- 1 Respostas
- 1391 Exibições
- Última mensagem por manuel_pato1

Qui Jan 17, 2013 23:18
Geometria Analítica
-
- Quádricas - Duas questões
por renan_a » Seg Jan 21, 2013 00:13
- 2 Respostas
- 5147 Exibições
- Última mensagem por renan_a

Qui Fev 07, 2013 08:43
Geometria Analítica
-
- [Cônicas]Retas tangentes à cônicas
por Hopkins » Ter Fev 28, 2017 22:39
- 0 Respostas
- 1521 Exibições
- Última mensagem por Hopkins

Ter Fev 28, 2017 22:39
Geometria Analítica
-
- Quadricas
por manuel_pato1 » Sex Jan 18, 2013 00:34
- 5 Respostas
- 3506 Exibições
- Última mensagem por Russman

Sex Jan 18, 2013 23:13
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 .Temos:
.Temos:
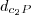 para o outro lado e o
para o outro lado e o 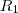 para o lado do
para o lado do  voce tera que a distancia de P aos centros e sempre uma constante que define uma hiperbole com foco nos centros das circunferencias.
voce tera que a distancia de P aos centros e sempre uma constante que define uma hiperbole com foco nos centros das circunferencias.
 ,teremos uma hipérbole pois os dois serão positivos ,pois:
,teremos uma hipérbole pois os dois serão positivos ,pois: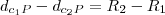 e como
e como  é constante segue a definição de hipérbole.
é constante segue a definição de hipérbole.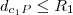 ou
ou .Teremos uma elipse e não importa qual vai ser menor os focos serão os mesmos e suas medidas também,pois:
.Teremos uma elipse e não importa qual vai ser menor os focos serão os mesmos e suas medidas também,pois: