 por Igor » Sex Dez 03, 2010 19:20
por Igor » Sex Dez 03, 2010 19:20
A soma e o produto das raízes do polinômio P(x)= 2x²+ bx+ c são, respectivamente, -6 e 5. Assim, o valor mínimo que P(x) pode assumir pertence ao conjunto:
A) { -6 , -4 , -1 }
B) {-5 , -3 , 0 }
C) { -8 , 1 , 6 }
D) { 2 , 4 , 5 }
E) { 3 , 7 , 8 }
Resolução:
Eu resolvi aplicando Girard , que x¹ + x² = -6, logo -b/2 = -6, portanto, b = 12 e x¹.x² = 5, logo (-1)² . c/2 = 5, portanto, c = 10. assim a equação fica P(x)= 2x² + 12x + 10, tendo como raízes resolvendo a expressão -1 e -5.
Mas, não sei qual resposta certa a marca pelo o que pede a questão. Se alguém puder me ajudar, obrigado pela força !
-
Igor
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Dom Nov 21, 2010 10:29
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Sáb Dez 04, 2010 18:43
por Molina » Sáb Dez 04, 2010 18:43
Boa tarde , Igor.
Você encontrou as raízes, tudo bem. Mas elas não serão utilizadas, já que a questão pede o ponto de mínimo. Como a > 0, este polinômio de 2° grau tem ponto de mínimo, ou seja, o menor ponto que p(x) vai assumir. Como é de segundo grau, você pode encontrar através do
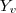
:
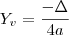

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Lorettto » Sáb Dez 04, 2010 19:24
por Lorettto » Sáb Dez 04, 2010 19:24
você precisa das raízes pra achar os valores de B e C , poderia ter feito um sistema para acha-los, mas também está correto fazer por GIRARD. Achando o 2x² + 12x + 10 , você acha o Delta e joga na Fórmula passada acima. Vai dar a alternativa C .
Abraço, Loreto.
-
Lorettto
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Sáb Nov 27, 2010 01:17
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Questão POSCOMP 2011] Ajuda para interpretar questão
por hlustosa » Dom Jul 29, 2012 14:54
- 3 Respostas
- 12987 Exibições
- Última mensagem por hlustosa

Seg Jul 30, 2012 01:13
Funções
-
- AJUDA NA QUESTÃO
por GABRIELA » Ter Set 08, 2009 16:00
- 1 Respostas
- 1448 Exibições
- Última mensagem por Molina

Ter Set 08, 2009 18:58
Matrizes e Determinantes
-
- AJUDA NA QUESTÃO...
por GABRIELA » Ter Out 20, 2009 16:28
- 1 Respostas
- 1142 Exibições
- Última mensagem por thadeu

Qua Out 21, 2009 12:12
Geometria Analítica
-
- Ajuda - Questão FCC
por cesilva » Qui Jan 31, 2013 12:36
- 2 Respostas
- 2682 Exibições
- Última mensagem por cesilva

Qui Jan 31, 2013 16:14
Lógica
-
- Ajuda na questão de Pré-Cálculo
por Jamilly » Ter Mar 16, 2010 10:12
- 5 Respostas
- 4347 Exibições
- Última mensagem por Jamilly

Qua Mar 17, 2010 20:24
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


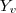 :
: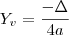





 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.