JUROS SIMPLES?

AjudaMatematica.com! Aqui você compartilha sua dúvida ou solução!

  • Anúncio Global
    Respostas
    Exibições
    Última mensagem

JUROS SIMPLES?

Regras do fórum
Responder

JUROS SIMPLES?

Mensagempor pamelasrodrigues » Qua Dez 01, 2010 11:58

Olá pessoal. Minha dúvida é quanto a questão abaixo, poderiam me ajudar na resolução?

Obtendo-se, em 15 meses, R$18.000,00 de juros simples pela aplicação de R$40.000,00 à taxa de 3% ao mês, qual o tempo necessário para se obter os mesmos juros, caso a taxa fosse de 30% ao ano?
pamelasrodrigues
Novo Usuário
Novo Usuário
 
Mensagens: 4
Registrado em: Ter Nov 30, 2010 20:53
Formação Escolar: GRADUAÇÃO
Área/Curso: CIÊNCIAS CONTÁBEIS
Andamento: cursando
Voltar ao topo

Re: JUROS SIMPLES?

Mensagempor alexandre32100 » Qua Dez 01, 2010 17:07

Olha, pelo que sei se a taxa é ao ano (a.a.) só temos geração de juros quando fechamos exatamente um ano. No caso 15 meses seriam apenas um ano. Mas o que queremos é o tempo que devemos deixar:
\\\J=Cit\\ 18000=40000\cdot0,3\cdot t\\ 18000=12000t\\ t=\frac{18}{12}=1,5
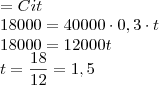
O que não entendo é que não há como aplicar durante um ano e meio - ou um ou dois anos.
alexandre32100
 
Voltar ao topo
Responder

Voltar para Matemática Financeira

 


Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!

  • Tópicos relacionados
    Respostas
    Exibições
    Última mensagem

Quem está online

Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 


Tópico Popular

Assunto: cálculo de limites
Autor: Hansegon - Seg Ago 25, 2008 11:29

Bom dia.

Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado

\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]

Assunto: cálculo de limites
Autor: Molina - Seg Ago 25, 2008 13:25

\lim_{x\rightarrow-1} \frac{{x}^{3}+1}{{x}^{2}-1}

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.

Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo. :y:

Caso ainda não tenha dado uma :idea:, avisa que eu resolvo.

Bom estudo!

Assunto: cálculo de limites
Autor: Guill - Dom Abr 08, 2012 16:03

\lim_{x\rightarrow-1}\frac{x^3+1}{x^2-1}

\lim_{x\rightarrow-1}\frac{(x+1)(x^2-x+1)}{(x+1)(x-1)}

\lim_{x\rightarrow-1}\frac{(x^2-x+1)}{(x-1)}=\frac{-3}{2}

Powered by phpBB © phpBB Group.

phpBB Mobile / SEO by Artodia.

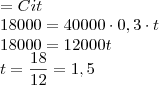
Índice do fórum