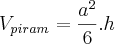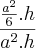A)1/3
B)1/4
C)1/6
D)1/8
E)1/12
A resposta correta é a C, mas eu tentei fazer e só consigo chegar na letra E.
Minha resolução fica assim;
O volume da pirâmide:
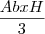
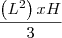 (já q a base da pirâmide está inserida numa caixa de base quadrada, logo a base da pirâmide é um quadrado)
(já q a base da pirâmide está inserida numa caixa de base quadrada, logo a base da pirâmide é um quadrado)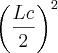 x
x 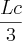 (eu coloquei lado da caixa sobre 2 pq ele diz q os vértices da base são os pontos médios das arestas do fundo da caixa e H=lado da caixa pq a piramide esta inserida na caixa e a ponta dela bate na tampa da caixa)
(eu coloquei lado da caixa sobre 2 pq ele diz q os vértices da base são os pontos médios das arestas do fundo da caixa e H=lado da caixa pq a piramide esta inserida na caixa e a ponta dela bate na tampa da caixa)Resolvendo fica:
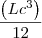
O volume da caixa é :
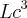
a razao:
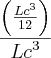
Aí vai ficar:

Não sei no que estou errando. Gostaria q alguém me ajudasse.


![d=l\sqrt[2]{2} d=l\sqrt[2]{2}](/latexrender/pictures/36913f394e0e1917e6c2b3db67122e35.png)
![a=l\sqrt[2]{2} a=l\sqrt[2]{2}](/latexrender/pictures/7591af6f527596fd2499f72ba054e0fb.png)
![l=\frac{a\sqrt[2]{2}}{a} l=\frac{a\sqrt[2]{2}}{a}](/latexrender/pictures/21854a97f9c8d2cadfc20285485e0eb5.png)
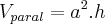
![{V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2} {V}_{piram}=\frac{1}{3}{\left(\frac{a\sqrt[2]{2}}{2} \right)}^{2}](/latexrender/pictures/096ca223c0fcfb2c064ee7db605ed269.png)