Alguém consegue encontrar outra maneira mais prática de resolver? Mais abaixo apresento minha resolução, agora, o exercício:
"Um triângulo ABC está inscrito numa circunferência de raio r. Se, num sistema de coordendas cartesianas, A = (1;3), B = (5;7) e C = (5;1), então r é igual a…"
(Resposta: O raio r = raiz quadrada de 10)
Gostaria de saber se há outra maneira de resolver, pois o jeito que encontrei foi muito trabalhoso e demorado. Se alguém souber, por favor, explique. Obrigado!
Minha maneira de resolução:
I. calculei a distância entre os pontos, ou seja, os lados AB, BC e CA do triângulo através da fórmula de distância entre dois pontos (resultando em 4 raiz de 2; 6 e 2 raiz de 5, respectivamente)
II. Como precisava saber o R, me lembrei de que a fórmula de área para um triângulo circunscrito pode ser Área = (a . b . c) / 4 raio. Mas, para poder isolar o raio, precisava de um valor para a área do triângulo.
III. Como só tinha o valor dos lados do triângulo, calculei a área através da looonga fórmula Área = raiz de (semiperímetro . (semiper -a) . (semiper – b) . (semiper – c)), o que resultou em Área = 12
IV. Substituindo agora o valor da área na fórmula mencionada na etapa II, cheguei a Raio = raiz de 10


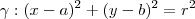
 e
e  e três pontos
e três pontos 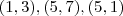 , acho que isto serve pra achar o valor do raio.
, acho que isto serve pra achar o valor do raio.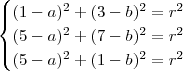


 .
.
 :
: