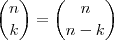 todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?

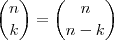 todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
todos nós sabemos, mas alguém sabe provar esta igualdade, sem, no entanto, usar-se da fórmula algébrica?
 corresponde à contagem de quantos grupos de
corresponde à contagem de quantos grupos de  elementos podemos formar a partir de um conjunto de
elementos podemos formar a partir de um conjunto de  . Esta mesma contagem pode ser feita escolhendo quais os
. Esta mesma contagem pode ser feita escolhendo quais os  elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),
elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),  grupos.
grupos.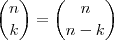 .
.alexandre32100 escreveu:Ah, um argumento seria o seguinte:corresponde à contagem de quantos grupos de
elementos podemos formar a partir de um conjunto de
. Esta mesma contagem pode ser feita escolhendo quais os
elementos que não farão parte dos grupos (e consequentemente os que não serão escolhidos farão parte),
grupos.
Assim conclui-se que.
 de elementos de
de elementos de  , haverá sempre um subconjunto complementar
, haverá sempre um subconjunto complementar  , daí que há a mesma quantidade destes subconjuntos..
, daí que há a mesma quantidade destes subconjuntos..
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.