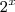 , usando a fórmula abaixo:
, usando a fórmula abaixo: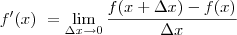
não consigo.. procurei pela fórmula de derivadas de exponenciais e a encontrei, mas detesto decorar algo sem saber por quê..
Ficaria muito grato se alguém pudesse demonstrá-la pra mim, já procurei em vários lugares e não achei demonstrações..


 . Veja:
. Veja: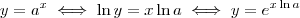
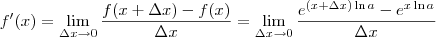

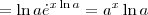
 para fazer aparecer o limite fundamental
para fazer aparecer o limite fundamental  .
. .
.


 .
.
 :
: