Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por victoreis1 » Seg Nov 22, 2010 21:26
por victoreis1 » Seg Nov 22, 2010 21:26
seja

uma função dos naturais nos naturais, tal que
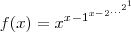
por exemplo,
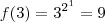
Deste modo, o último dígito, na base decimal, de f(2009) é?
tem como calcular isso usando aritmética modular? Oo
edit: fiz aqui e deu 1, não sei se tá certo..
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Nov 22, 2010 23:14
por Molina » Seg Nov 22, 2010 23:14
Boa noite, Victor.
Vou dar uma dica que espero que seja esse o caminho e acredito que vá ajudar.
Perceba que:
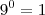
(
um)
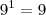
(
nove)

(oitenta e
um)

(setecentos e vinte e
nove)
.
.
.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por victoreis1 » Seg Nov 22, 2010 23:23
por victoreis1 » Seg Nov 22, 2010 23:23
molina escreveu:Boa noite, Victor.
Vou dar uma dica que espero que seja esse o caminho e acredito que vá ajudar.
Perceba que:
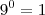
(
um)
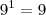
(
nove)

(oitenta e
um)

(setecentos e vinte e
nove)
.
.
.

exatamente, vi que
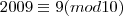
, e, portanto,
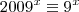
(mod 10)
daí vi que x era par, visto que x é múltiplo de 2008, logo
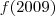
termina com 1. certo?
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Seg Nov 22, 2010 23:54
por Molina » Seg Nov 22, 2010 23:54
No meu entendimento é isso sim, Victor.
Para garantir vou começar a fazer num papelzinho, quando eu terminar te aviso!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- DESAFIO DE QUEM É O MAIS SÁBIO DO FÓRUM
por tenebroso » Qua Dez 18, 2013 16:15
- 1 Respostas
- 1188 Exibições
- Última mensagem por tenebroso

Qua Dez 18, 2013 16:43
Probabilidade
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5649 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
-
- Desafio dos Dez Pontos
 por Molina » Sáb Jul 12, 2008 00:02
por Molina » Sáb Jul 12, 2008 00:02
- 6 Respostas
- 5282 Exibições
- Última mensagem por admin

Dom Jul 13, 2008 17:00
Desafios Fáceis
-
- Desafio de lógica
por Twister » Qua Ago 13, 2008 21:46
- 10 Respostas
- 10008 Exibições
- Última mensagem por andymath

Qua Mar 31, 2010 19:14
Desafios Enviados
-
- Desafio do relógio
por ericomoura » Ter Nov 17, 2009 12:03
- 9 Respostas
- 8299 Exibições
- Última mensagem por Dan

Qui Fev 10, 2011 12:21
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 uma função dos naturais nos naturais, tal que
uma função dos naturais nos naturais, tal que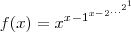
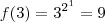

 uma função dos naturais nos naturais, tal que
uma função dos naturais nos naturais, tal que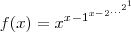
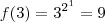

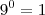 (um)
(um)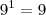 (nove)
(nove) (oitenta e um)
(oitenta e um) (setecentos e vinte e nove)
(setecentos e vinte e nove)
(um)
(nove)
(oitenta e um)
(setecentos e vinte e nove)
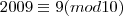 , e, portanto,
, e, portanto, 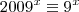 (mod 10)
(mod 10)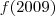 termina com 1. certo?
termina com 1. certo?

 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
