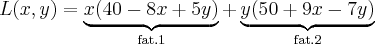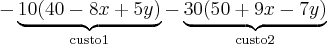[otimização] DERIVADAS PARCIAIS

por **montanha** » Seg Ago 04, 2008 10:18

Pessoal

Estou com dificuldade no exercicio abaixo, alguém pode me ajudar a responder a questão 1 e 2

A companhia telefônica está lançando dois novos tipos de sistemas de comunicação para executivos, que pretendem vender a grandes empresas. Estima-se que, se o preço de um dos sistemas for x centenas de reais e o preço do outro for y centenas de reais, serão vendidos 40 – 8x + 5y sistemas do primeiro tipo e 50 + 9.x – 7.y do segundo. O custo de fabricação do primeiro tipo de sistema é R$ 1.000,00 e o do segundo é R$ 3.000,00.

1) Os acionistas desejam saber: Quanto a companhia deverá cobrar pelo sistema 1 (em centenas de reais) para obter o maior lucro possível?
a) 3.156,00
b) 3.000,00
c) 3.896,00
d) 3.545,00
e) 3.320,00

2) E quanto deverá cobrar pelo sistema 2 (em centenas de reais)?
a) 4.500,00
b) 4.483,10
c) 4.664,57
d) 4.605,50
e) 4.308,41

por **admin** » Seg Ago 04, 2008 16:37

Olá montanha, boas-vindas!

montanha escreveu:Estou com dificuldade no exercicio abaixo, alguém pode me ajudar...

Eu resolvi os problemas e "imagino" quais as prováveis dúvidas relacionadas, mas é importante você especificar a dificuldade e citar até qual ponto conseguiu chegar. Assim acredito que poderemos tornar a interação mais interessante para seu estudo.

Como não sei em qual aspecto está a sua dificiculdade, de antemão, fica como dica iniciar tentando representar a função do lucro.
Pense da forma mais simples possível. Pergunta: o que é lucro? Resposta: faturamento menos custo!

Ou seja, passo a passo, identifique:

a expressão do faturamento 1 (do sistema 1);
a expressão do faturamento 2 (do sistema 2);
a expressão do custo 1 (do sistema 1);
a expressão do custo 2 (do sistema 2).

Quando você conseguir identificar estas expressões, monte a função lucro:
lucro = faturamento1 + faturamento2 - custo1 - custo2

Cuidado: utilize os valores dos custos em centenas de reais!

Após esta etapa, também é interessante perceber que sendo a função lucro

uma curva parabólica, côncava para baixo, quando buscamos o valor máximo, associamos à derivada, pois no ponto máximo, o plano tangente será paralelo ao plano xy, ou seja, sua inclinação será nula, ou ainda, a derivada (que fornece a inclinação do plano tangente no ponto) também deverá ser nula.

Após fazer as duas derivadas parciais e pela condição de interesse comentada acima, igualando-as a zero, você obterá um sistema linear com duas equações e duas incógnitas x e y, cujos valores representam centenas de reais.

Enfim, farei um pausa por aqui pois, como disse, não sei qual a sua dúvida.
Aguardo seus comentários e bons estudos!

por **montanha** » Ter Ago 05, 2008 18:20

Olá Fabio

Então na verdade eu aprendi derivadas a vários anos atrás e estou fazendo um teste a longa distancia, que caiu essa questão, então precisava saber qual das alternativas é a correta. Na verdade não sei nem por onde começar....

por **admin** » Ter Ago 05, 2008 18:30

Olá, boa tarde.
Sobre "por onde começar", fica minha dica anterior.
Será fundamental revisar a teoria e trabalhar no percurso comentado, em busca de algum entendimento.

Como fruto e conseqüência natural de seus estudos, as dúvidas surgirão e serão bem-vindas aqui.

Bons estudos!

por **montanha** » Sex Ago 08, 2008 14:43

Fabio

Consegui resolver dessa maneira, leia a observação

Primeiramente, necessitamos saber o Lucro total, que é dado pelo Lucro com as vendas do sistema 01 + Lucro com as vendas do sistema 02.
Com isso, sabemos que o lucro com a venda dos sistemas é calculado por meio do (nº de sistemas vendidos).(lucro por unidade).
O lucro por unidade é obtido pelo preço de venda - preço de custo.

Como o primeiro tipo de sistema é vendido por x centenas de reais e tem um custo de fabricação de R$ 1.000,00 (ou 10 centenas de reais), o lucro por sistema vendido é (x - 10). Como a demanda do primeiro sistema é 40 - 8x + 5y, o lucro com a venda desse tipo de sistema é:

P1 = (x - 10).(40 - 8.x + 5y)

O segundo tipo de sistema é vendido por y centenas de reais e tem um custo de fabricação de R$ 3.000,00 (ou 30 centenas de reais). Como a demanda do segundo sistema é 50 + 9x - 7y, o lucro com a venda desse tipo de sistema é:

P2 = (y - 30).(50 + 9.x - 7y)

Assim, o lucro total é:

P(x,y) = P1 + P2 = (x - 10).(40 - 8.x + 5y) + (y - 30).(50 + 9.x - 7y)
Aplicando a distributiva e rearranjando os termos semelhantes, temos:
P(x,y) = 40.x - 8.x2 + 5.yx - 400 + 80.x - 50.y + 50.y + 9.xy - 7.y2 - 1500 - 270.x + 210.y
P(x,y) = -150.x -8.x2 + 14.xy - 1900 + 210.y - 7y2

Vamos agora calcular as derivadas parciais do lucro para saber quanto a companhia deve cobrar por cada sistema:

Px = -150 - 16x + 14y e
Py = 14x + 210 - 14y

que são iguais a 0 para:

-150 - 16x + 14y = 0
210 + 14x - 14y = 0

Somando as duas equações, obtemos 60 - 2x = 0 ou x = 30. Fazendo x = 30 na primeira equação, obtemos -150 - 16(30) + 14y = 0, 14y = 630 ou y = 45.

Assim, para maximizar o lucro, a companhia telefônica deverá cobrar R$3.000,00 pelo primeiro sistema (x = 30 centenas de reais) e R$4.500,00 pelo segundo (y = 45 centenas de reais).

por **admin** » Sex Ago 08, 2008 15:14

Olá.
A resolução está correta.

Apenas devo comentar que também iniciando por:
lucro = faturamento1 + faturamento2 - custo1 - custo2

$L(x,y) = \underbrace{x(40-8x+5y)}_{\text{fat.1}} + \underbrace{y(50+9x-7y)}_{\text{fat.2}}$ $- \underbrace{10(40-8x+5y)}_{\text{custo1}} - \underbrace{30(50+9x-7y)}_{\text{custo2}}$

Colocando fatores em evidência, analogamente chegamos ao seu ponto de partida:

$L(x,y) = \underbrace{(x-10)(40-8x+5y)}_{\text{lucro1}} + \underbrace{(y-30)(50+9x-7y)}_{\text{lucro2}}$

Aparentemente, não há dúvidas. Até mais!