 por Bruhh » Ter Nov 09, 2010 17:09
por Bruhh » Ter Nov 09, 2010 17:09
[i]Olá

Estou tendo dificuldades em resolver esses dois problemas. Creio que, por eles serem parecidos, a resolução
seja a mesma, porém não consigo resolver nenhum dos dois.
1-R:3,6
2-R:0,08pi
Como eu determino
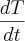
??
Pela regra da cadeia? Pelo conceito de diferencial total?
Que incognita devo derivar?
Obrigada *-*
-
Bruhh
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Seg Mar 01, 2010 14:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Eng. Química
- Andamento: cursando
 por Marcampucio » Ter Nov 09, 2010 20:27
por Marcampucio » Ter Nov 09, 2010 20:27
QUESTÃO 8:

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Que método usar para resolver esse problema?
por souzalucasr » Seg Mai 07, 2012 12:43
- 1 Respostas
- 1625 Exibições
- Última mensagem por LuizAquino

Seg Mai 07, 2012 18:17
Cálculo: Limites, Derivadas e Integrais
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3702 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- [Derivada] Funciona para produto mas não para quociente?
por Matheus Lacombe O » Ter Dez 11, 2012 23:46
- 1 Respostas
- 2189 Exibições
- Última mensagem por Russman

Qua Dez 12, 2012 01:39
Cálculo: Limites, Derivadas e Integrais
-
- [m.m.c.] Problemas para ajudar uma criança!
por aline1805 » Seg Jun 23, 2008 19:56
- 6 Respostas
- 8339 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 04:09
Álgebra Elementar
-
- Ajuda para resolver!!
por Optikool » Dom Dez 02, 2012 21:31
- 2 Respostas
- 3200 Exibições
- Última mensagem por Optikool

Ter Dez 04, 2012 22:22
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 ??
??



