


arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL


molina escreveu:arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL
Boa tarde, Arima.
Confirma o enunciado, o certo seria: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É IRRACIONAL
Né?!

 é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,
é racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,  é da forma
é da forma  irredutível, com
irredutível, com  ,
, 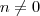 :
:

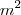 é divisível por
é divisível por  e consequentemente
e consequentemente  é divisível por
é divisível por  .
. , com
, com 


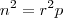
 é divisível por
é divisível por  e consequentemente
e consequentemente  é divisível por
é divisível por  .
. era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
era irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p). não é da forma
não é da forma  e com isso é IRRACIONAL.
e com isso é IRRACIONAL.


molina escreveu:Boa noite.
Esta demonstração se prova por absurdo. Comece supondo queé racional (é isto que no final você vai contradizer e concluir que é irracional). Logo,
é da forma
irredutível, com
,
:
Logoé divisível por
e consequentemente
é divisível por
.
Então, podemos escrever, com
Com isso temos que:
Logoé divisível por
e consequentemente
é divisível por
.
Com isso temos um absurdo, por assumimos inicialmente queera irredutível, ou seja, primos entre si. E o que acabamos de mostrar que eles tem um múltiplo em comum (p).
Assim, nossa hipótese é negada e temos quenão é da forma
e com isso é IRRACIONAL.
Caso tenha dúvida em alguma passagem, informe!
Bom estudo,

arima escreveu:qUEM PODE ME AJUDAR OBRIGADA: SENDO P NUMERO PRIMO PROVE QUE RAIZ DE P É RACIONAL


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)