Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Pedro123 » Dom Out 31, 2010 22:35
por Pedro123 » Dom Out 31, 2010 22:35
kkkk minha resposta deu 2. está certo?
fiz assim Y = 2^1/2 . 2^1/4 . 2^1/8.... = 2^1/2+1/4+1/8.... -->
Pela soma de PG infinita temos:
S = 1/2 / 1-1/2 = 1
Portanto Y = 2
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por GeRmE » Sex Nov 05, 2010 19:05
por GeRmE » Sex Nov 05, 2010 19:05
seu chato XD
é isso mesmo, mas o meu método é mais legal:
eleva-se os dois lados ao quadrado e têm-se:
![Y^2= \left(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} \right)^2 Y^2= \left(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} \right)^2](/latexrender/pictures/b07215bd9a50bfceb010a50cae0fc494.png)
depois:
![Y^2=2.(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} ) Y^2=2.(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} )](/latexrender/pictures/2b33455f11bc434eb5fb0bdfc0220d92.png)
se
![Y=\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.}...}}}}} Y=\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.}...}}}}}](/latexrender/pictures/4fb791f67dea0f6fd606ec18cae8d024.png)
então
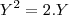
logo

e

-

GeRmE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Out 29, 2010 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estidante de medicina
- Andamento: cursando
 por Pedro123 » Sex Nov 19, 2010 12:10
por Pedro123 » Sex Nov 19, 2010 12:10
hahahaha realmente, seu método é mais criativo, não pensei nisso hsuahuahs
mas é isso ae abrass hahaha
-
Pedro123
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qui Jun 10, 2010 22:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica - 1° Período
- Andamento: cursando
 por alexandre32100 » Sex Nov 19, 2010 13:41
por alexandre32100 » Sex Nov 19, 2010 13:41
GeRmE escreveu: cá entre nós,resolve-se em três linhas
Qual o tamanho de suas linhas? Não consigo colocar um expressão deste tamanho numa linha só. lol
Mas fiz uma terceira solução
GeRmE escreveu:![Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}} Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}}](/latexrender/pictures/99978ae64d56c2794a5cafa6efa67994.png)
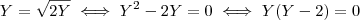

e

.
OPA! Alguma coisa errada. Por que

não pode ser igual a

?
-
alexandre32100
-
 por MarceloFantini » Sex Nov 19, 2010 14:22
por MarceloFantini » Sex Nov 19, 2010 14:22
Impossível extrair a raíz quadrada de um número diferente de zero e obter zero.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por GeRmE » Sex Nov 19, 2010 16:36
por GeRmE » Sex Nov 19, 2010 16:36
bom, pelo menos o 2 apareceu. ao final de um exercício desses o certo é verificar, o que fica meio complicado...
-

GeRmE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Out 29, 2010 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estidante de medicina
- Andamento: cursando
 por alexandre32100 » Sex Nov 19, 2010 17:32
por alexandre32100 » Sex Nov 19, 2010 17:32
Fantini escreveu:Impossível extrair a raíz quadrada de um número diferente de zero e obter zero.
Mas se
![0= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}} 0= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}}](/latexrender/pictures/69907bd5d71938cc97d45f1bb1b0d43f.png)
, é lógico dizer também que
![2\cdot0={2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}} 2\cdot0={2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}](/latexrender/pictures/1e801cd6be8f33d96faf5f5d6900bb2a.png)
, ou seja, estamos extraindo a raiz quadrada de

, logo a expressão é igual a

.
-
alexandre32100
-
 por MarceloFantini » Sex Nov 19, 2010 17:36
por MarceloFantini » Sex Nov 19, 2010 17:36
Não, não é, pois
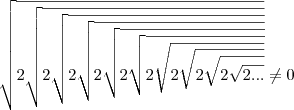
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por GeRmE » Sex Nov 19, 2010 18:49
por GeRmE » Sex Nov 19, 2010 18:49
amigo, o Zero é um número anormal. quer um exemplo? veja: 2 = 3 pois 0.2=0.3
quando a resposta der zero, desconfie
-

GeRmE
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Sex Out 29, 2010 15:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estidante de medicina
- Andamento: cursando
Voltar para Desafios Enviados
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- É muito difícil
por Thiago 86 » Dom Set 29, 2013 21:21
- 2 Respostas
- 2752 Exibições
- Última mensagem por Thiago 86

Sex Out 04, 2013 10:11
Funções
-
- Muito dificil
por Maria da Silva » Qui Dez 19, 2013 17:13
- 0 Respostas
- 2457 Exibições
- Última mensagem por Maria da Silva

Qui Dez 19, 2013 17:13
Análise Combinatória
-
- piada não muito matemática
por [++] » Dom Jul 19, 2009 23:29
- 2 Respostas
- 3468 Exibições
- Última mensagem por antonybel

Sex Nov 11, 2011 13:18
Piadas
-
- Questão Muito Tensa
por nandokmx » Qui Mai 20, 2010 10:45
- 1 Respostas
- 1991 Exibições
- Última mensagem por Douglasm

Qui Mai 20, 2010 12:21
Estatística
-
- Matrizes e cia muito dificil de resolver.
por elisonsevalho » Sex Mar 05, 2010 17:35
- 2 Respostas
- 3453 Exibições
- Última mensagem por Douglasm

Sex Mar 05, 2010 19:03
Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}} Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}}](/latexrender/pictures/99978ae64d56c2794a5cafa6efa67994.png)


![Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}} Y= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}}](/latexrender/pictures/99978ae64d56c2794a5cafa6efa67994.png)


![Y^2= \left(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} \right)^2 Y^2= \left(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} \right)^2](/latexrender/pictures/b07215bd9a50bfceb010a50cae0fc494.png)
![Y^2=2.(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} ) Y^2=2.(\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}} )](/latexrender/pictures/2b33455f11bc434eb5fb0bdfc0220d92.png)
![Y=\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.}...}}}}} Y=\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.\sqrt[2]{2.}...}}}}}](/latexrender/pictures/4fb791f67dea0f6fd606ec18cae8d024.png)
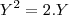




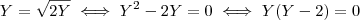
 e
e  .
. não pode ser igual a
não pode ser igual a  ?
?


![0= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}} 0= \sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}}](/latexrender/pictures/69907bd5d71938cc97d45f1bb1b0d43f.png) , é lógico dizer também que
, é lógico dizer também que ![2\cdot0={2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}} 2\cdot0={2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2\sqrt[2]{2}...}}}}}}}](/latexrender/pictures/1e801cd6be8f33d96faf5f5d6900bb2a.png) , ou seja, estamos extraindo a raiz quadrada de
, ou seja, estamos extraindo a raiz quadrada de  , logo a expressão é igual a
, logo a expressão é igual a  .
.
