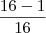Olá!
Tenho um problema de probabilidade do 9º ano que não consigo entender! É o seguinte:
Se lançarmos uma moeda 4 vezes, qual a probabilidade de obter CARA nos quatro lançamentos?
Na solução do problema o autor montou um diagrama de árvore que eu não consigo entender.
Disse ainda que são 16 resultados possíveis e que para cada lançamento há duas possibilidades: 2.2.2.2=16 possibilidades no total. Ele diz que a probabilidade de obter CARA é de 1/16.
Não tenho conseguido entender pq 16 possibilidades e nem o diagrama de árvore (em anexo).
Abraços
Clau



 =32, 32 seria o número de possiblidades. Mas, como saber o número de possibilidades favoráveis sem o diagrama de árvore?
=32, 32 seria o número de possiblidades. Mas, como saber o número de possibilidades favoráveis sem o diagrama de árvore?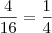 .
.