estou cursando o ensino medio tec. materia nova um trabalho e nao estou conseguindo chega a lugar algum!
PRESISO DO RESULTADO I DA RESOLUÇAO!
1) Sendo 0
 x < 2
x < 2
A) Sen X =
![\sqrt[]{2}/2 \sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png)
B) Cos X = -
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)
C) Sen x = -1
D) Cos X = -1

 x < 2
x < 2
![\sqrt[]{2}/2 \sqrt[]{2}/2](/latexrender/pictures/8450365496cb8076b83d7e1458c1a146.png)
![\frac{\sqrt[]{3}}{2} \frac{\sqrt[]{3}}{2}](/latexrender/pictures/21682d7c1e802e9b52a99c01850489c4.png)



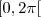

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)