Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por zinho » Qui Ago 19, 2010 17:00
por zinho » Qui Ago 19, 2010 17:00
Pessoal tudo bem?Estou precisando de uma ajudinha no calculo de expressões numéricas,segundo a regra primeiro tenho que resolver os parênteses,depois as chaves,depois os colchetes,ai então eu resolvo as multipicações e divisões e por ultimo as adições e subtrações.Mas partindo deste princípio não estou conseguindo resolver esta expressão.

A resposta segundo a lista passada pelo meu professor é a seguinte
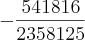
ou
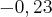
Pessoal se alguem puder me ajudar desde já agradeço
-
zinho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Ago 19, 2010 13:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de informação
- Andamento: cursando
 por alexandre32100 » Qui Ago 19, 2010 18:59
por alexandre32100 » Qui Ago 19, 2010 18:59
Não gosto muito dessas expressões porque geralmente me enrolo, troco um número e me dou mal.
Fazendo "na mão" cheguei ao resultado
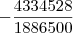
(a qual você chegou, Zinho?) e conferi usando o computador, deu o mesmo:

.
Posso estar enganado, mas acho que o resultado é este.

-
alexandre32100
-
 por Elcioschin » Qui Ago 19, 2010 19:03
por Elcioschin » Qui Ago 19, 2010 19:03
Numerador da 1ª expressão:
3 - 2/5 = 15/5 - 2/5 = 13/5 ----> (1/2)*(13/5) = 13/10 ----> 4/7 + 13/10 = 40/70 + 91/70 = 131/70
Denominador da 1ª expressão: 1 - 3 = - 2 ----> (1/4)*(-2) = - 1/2 ---> 25 - 1/2 = 50/2 - 1/2 = 49/2
Resultado da 1ª expressão ----> (131/70)/(49/2) = (131/70)*(2/49) = 131/1715
Numerador da 2ª expressão: 1/4 - 3 = 1/4 - 12/4 = - 11/4 ----> (5/8)*(-11/4) = - 5*11/32
Denominador da 2ª expressão: 0,17 + 5 = 5,17 = 517/100 = 11*47/100
Resultado da 2ª expressão: (- 5*11/32)/(11*47/100) = (- 5*11/32)*(100/11*47) = - 5*25/8*47 = - 125/376
Expressão final ----> (131/1715)/(-125/376) = (131/1715)*(-376/125) = - (131*376)/(1715*125) = 49256/214375
Como vc pode ver o meu resultado não "bateu" com o seu gabarito. Por favor confira as contas o gabarito;
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por zinho » Qui Ago 19, 2010 21:22
por zinho » Qui Ago 19, 2010 21:22
Gente muito obrigado pela ajuda,conversei com mais alguns colegas e eles confirmaram que o professor disse que o gabarito estava mesmo errado,mais uma vez muito obrigado gente.
-
zinho
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Qui Ago 19, 2010 13:00
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de informação
- Andamento: cursando
Voltar para Problemas do Cotidiano
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- expressões numéricas
por karenblond » Qui Abr 14, 2011 16:22
- 1 Respostas
- 1340 Exibições
- Última mensagem por Abelardo

Qui Abr 14, 2011 19:58
Funções
-
- expressões numéricas
 por karenblond » Qui Abr 14, 2011 16:22
por karenblond » Qui Abr 14, 2011 16:22
- 7 Respostas
- 4221 Exibições
- Última mensagem por FilipeCaceres

Sex Abr 15, 2011 21:28
Funções
-
- expressoes numericas
por natyfofinha123456 » Qua Mar 28, 2012 16:41
- 0 Respostas
- 992 Exibições
- Última mensagem por natyfofinha123456

Qua Mar 28, 2012 16:41
Funções
-
- expressoes numericas
por natyfofinha123456 » Qua Mar 28, 2012 16:41
- 1 Respostas
- 1734 Exibições
- Última mensagem por DanielFerreira

Sáb Mar 31, 2012 18:11
Funções
-
- expressoes numericas
por natyfofinha123456 » Qua Mar 28, 2012 17:13
- 2 Respostas
- 1510 Exibições
- Última mensagem por profmatematica

Qui Mar 29, 2012 00:06
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

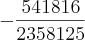
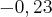


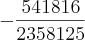
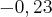

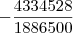 (a qual você chegou, Zinho?) e conferi usando o computador, deu o mesmo:
(a qual você chegou, Zinho?) e conferi usando o computador, deu o mesmo:  .
.

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.