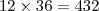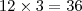Seção para postagens de problemas matemáticos do cotidiano, reportagens, casos interessantes, polêmicos ou curiosos.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por Alessandra Cezario » Seg Mai 02, 2011 16:52
por Alessandra Cezario » Seg Mai 02, 2011 16:52
Oi!Comecei estudar problemas do segundo grau e logo de cara já sinto dúvida.
O produto de dois números é 432. Determine esses números, sabendo-se que um é triplo do outro.
( o produto de dois números é x.y=432 ou x.3y?) ou pensei ainda em x.(3 -x).Sei que é fácil, mas não consigo fazer, me dá uma luz/
-
Alessandra Cezario
- Usuário Ativo

-
- Mensagens: 24
- Registrado em: Qui Mar 31, 2011 19:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em Português
- Andamento: formado
 por TheoFerraz » Seg Mai 02, 2011 17:29
por TheoFerraz » Seg Mai 02, 2011 17:29
Chamaremos os numeros de X e de Y.
Se o produto deles é 432 voce pode escrever :
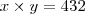
E se um é o triplo do outro, voce pode escrever :
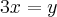
Bom, a partir dai voce tem um sisteminha simples. substitua na primeira equação o ' y ' que voce obteve na segunda equação,
Obtendo:
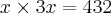
Dai,

Voce pode dividir ambos os lados por 3 para obter:
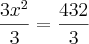
dai obtendo que :
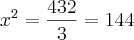
Agora tirando a raiz quadrada de abos os lados fica :
![\sqrt[2]{{x}^{2}} = \sqrt[2]{144} \sqrt[2]{{x}^{2}} = \sqrt[2]{144}](/latexrender/pictures/14020e0381d3624a8a0addf386444f54.png)
Cancelando as raizes do primeiro termo obtém-se:
![x = \sqrt[2]{144} x = \sqrt[2]{144}](/latexrender/pictures/66de02cb691aa290e55a7b47cdb1d188.png)
Resultando em

Para completar se:
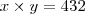
sabemos entao que

portanto,

resultando em:

Observe que a resposta é coerente!
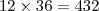
e
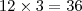
Espero ter ajudado.
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
Voltar para Problemas do Cotidiano
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação do segundo grau, problema dúvida!
 por LuizCarlos » Dom Mai 13, 2012 19:28
por LuizCarlos » Dom Mai 13, 2012 19:28
- 5 Respostas
- 3333 Exibições
- Última mensagem por DanielFerreira

Sáb Mai 19, 2012 10:20
Álgebra Elementar
-
- Função do segundo grau
por gustavoluiss » Dom Nov 28, 2010 17:27
- 7 Respostas
- 5519 Exibições
- Última mensagem por alexandre32100

Qua Dez 01, 2010 15:39
Álgebra Elementar
-
- Equação do segundo grau
por VtinxD » Qui Jan 27, 2011 23:03
- 1 Respostas
- 3885 Exibições
- Última mensagem por douglaspezzin

Dom Jun 19, 2011 09:55
Desafios Médios
-
- Inequação do segundo grau
por Aliocha Karamazov » Ter Abr 05, 2011 21:42
- 4 Respostas
- 4680 Exibições
- Última mensagem por Aliocha Karamazov

Qua Abr 06, 2011 18:51
Funções
-
- Inequação de segundo grau
por Aliocha Karamazov » Ter Abr 12, 2011 18:22
- 1 Respostas
- 1483 Exibições
- Última mensagem por FilipeCaceres

Ter Abr 12, 2011 19:53
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


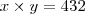
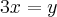
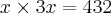

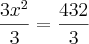
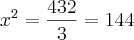
![\sqrt[2]{{x}^{2}} = \sqrt[2]{144} \sqrt[2]{{x}^{2}} = \sqrt[2]{144}](/latexrender/pictures/14020e0381d3624a8a0addf386444f54.png)
![x = \sqrt[2]{144} x = \sqrt[2]{144}](/latexrender/pictures/66de02cb691aa290e55a7b47cdb1d188.png)