Materiais sobre Estatística.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por freddurao » Ter Mar 01, 2011 16:59
por freddurao » Ter Mar 01, 2011 16:59
Entao pessoal, perdao pela minha ignorancia no assunto.
Mas meu objetivo é simples: Tenho duas curvas e quero medir a diferenca entre elas. Como nao tenho a funcao das curvas, nao posso medir a integral.
Mas tenho os pontos das curvas, entao fui sugerido a calcular o MSE. Beleza ate ai.
O mean squared error (MSE) no entanto necessita que eu calcule a diferenca de um ponto estimado (por uma funcao estimadora) e o ponto de cada uma das curvas.
Minha questao é? Como definir essa funcao estimadora? Essa informacao que eu nao consigo encontrar.
Se alguem puder ajudar eu agradeco.
-
freddurao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 01, 2011 16:51
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Computacao
- Andamento: formado
 por LuizAquino » Ter Mar 01, 2011 17:40
por LuizAquino » Ter Mar 01, 2011 17:40
Digamos que uma curva seja formada pelos pontos

e a outra pelos pontos
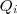
, com i=1, ..., N, sendo que eles seguem um mesmo sentido sobre o contorno das curvas. Uma forma bem simples de "medir" quão próximo uma curva está da outra é fazer:

Quanto mais
d for próximo de zero, mais as curvas devem estar próximas. Dependendo do que você quer, isso já pode ser o suficiente.
Há como você postar aqui o gráfico dessas curvas?
Editado pela última vez por
LuizAquino em Ter Mar 01, 2011 17:51, em um total de 1 vez.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por freddurao » Ter Mar 01, 2011 17:50
por freddurao » Ter Mar 01, 2011 17:50
Muito obrigado pela ajuda.
Mas em relacao a questao da funcao que faz a estimativa do ponto. Qual seria uma maneira de eu encontra-la?
Muito grato.
-
freddurao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 01, 2011 16:51
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Computacao
- Andamento: formado
 por LuizAquino » Ter Mar 01, 2011 17:57
por LuizAquino » Ter Mar 01, 2011 17:57
Você tem duas curvas e quer "medir" quão próxima elas estão usando o MSE. Eu acredito que uma opção seja você usar uma curva como se fosse a função estimadora e a outra como a função real.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por freddurao » Ter Mar 01, 2011 18:08
por freddurao » Ter Mar 01, 2011 18:08
Entendo o seu ponto de vista.
Mas minha idea é calcular um ponto otimo que cada ponto poderia atingir. Isso seria dado por essa funcao estimadora.
MInha intencao é calcular o quao cada uma das curvas esta distante da curva otima.. digamos assim.
Obrigado.
-
freddurao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 01, 2011 16:51
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Computacao
- Andamento: formado
 por LuizAquino » Ter Mar 01, 2011 23:37
por LuizAquino » Ter Mar 01, 2011 23:37
Não dá para adivinhar qual seria o formato dessa função estimadora sem ver as curvas que você deseja comparar. Ou ainda, sem conhecer o problema que gerou essas curvas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por freddurao » Qua Mar 02, 2011 12:21
por freddurao » Qua Mar 02, 2011 12:21
A foto das curvas segue em anexo.
As duas curvas compartilham o mesmos valores X, a diferenca é o Y, ou seja altura do pontos.
O valor máximo é 1, o máximo. O que eu poderia fazer seria justamente fazer a diferenca de cada 1-Py e 1-Qy.
Mas o fato é que 1 nao é necessariamente um ponto esperado para nenhuma das curvas dado o historico delas. Por isso que nao quero simplismente dizer que 1 vai ser o resultado (sempre) da minha funcao estimadora.
abs,
Você não está autorizado a ver ou baixar esse anexo.
-
freddurao
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Ter Mar 01, 2011 16:51
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Computacao
- Andamento: formado
 por LuizAquino » Qua Mar 02, 2011 12:39
por LuizAquino » Qua Mar 02, 2011 12:39
A "cara" dessas curvas lembram-me um logaritmo. Veja a figura abaixo.
função-ln.png
É claro que você ainda teria que modificar essa função para atender as suas necessidades.
Você não está autorizado a ver ou baixar esse anexo.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Estatística
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Como definir medidas (metragens)
por sirlenibatista » Seg Mai 03, 2010 21:57
- 1 Respostas
- 1592 Exibições
- Última mensagem por MarceloFantini

Ter Mai 04, 2010 13:03
Cálculo: Limites, Derivadas e Integrais
-
- Como definir a relação de um conjunto?
por baianinha » Ter Mai 17, 2011 22:31
- 0 Respostas
- 1108 Exibições
- Última mensagem por baianinha

Ter Mai 17, 2011 22:31
Conjuntos
-
- [Integral dupla]definir região de integração
 por jeferson_justo135 » Qua Jan 14, 2015 21:17
por jeferson_justo135 » Qua Jan 14, 2015 21:17
- 8 Respostas
- 6107 Exibições
- Última mensagem por jeferson_justo135

Seg Fev 09, 2015 17:07
Cálculo: Limites, Derivadas e Integrais
-
- [Integral tripla]definir valores para cálculo
 por jeferson_justo135 » Qua Jan 14, 2015 21:24
por jeferson_justo135 » Qua Jan 14, 2015 21:24
- 5 Respostas
- 3458 Exibições
- Última mensagem por jeferson_justo135

Dom Fev 08, 2015 15:51
Cálculo: Limites, Derivadas e Integrais
-
- Definir qual tipo de triângulo - Atividade com vetores.
por Raphaelphtp » Qua Jan 11, 2017 20:38
- 2 Respostas
- 1898 Exibições
- Última mensagem por Raphaelphtp

Sex Jan 13, 2017 19:11
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e a outra pelos pontos
e a outra pelos pontos 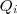 , com i=1, ..., N, sendo que eles seguem um mesmo sentido sobre o contorno das curvas. Uma forma bem simples de "medir" quão próximo uma curva está da outra é fazer:
, com i=1, ..., N, sendo que eles seguem um mesmo sentido sobre o contorno das curvas. Uma forma bem simples de "medir" quão próximo uma curva está da outra é fazer:
