MAT1351
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por scggomes » Sex Abr 15, 2011 16:38
por scggomes » Sex Abr 15, 2011 16:38
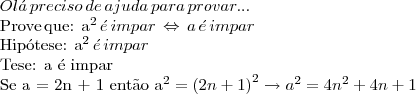
Como eu faço a volta, ou seja, se e somente se ?
Obrigada.
Cris
-
scggomes
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 18, 2011 10:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: formado
 por LuizAquino » Sex Abr 15, 2011 17:13
por LuizAquino » Sex Abr 15, 2011 17:13
Você vai precisar usar o fato (cuja a prova é simples) de que se
ab é par, então
a é par ou
b é par.
Sabemos que se

é ímpar, então

para algum k natural.
Mas, isso é o mesmo que

.
Agora, tente terminar usando as informações dadas.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por MarceloFantini » Sex Abr 15, 2011 19:48
por MarceloFantini » Sex Abr 15, 2011 19:48
Lembre-se do jeito de usar absurdo: suponha

par e veja uma contradição.
Editado pela última vez por
MarceloFantini em Sex Abr 15, 2011 20:05, em um total de 2 vezes.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por scggomes » Sex Abr 15, 2011 19:51
por scggomes » Sex Abr 15, 2011 19:51
Ainda não entendi como terminar, fiquei ainda mais confusa...
Cris
-
scggomes
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Fev 18, 2011 10:13
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Sistemas de Informação
- Andamento: formado
 por MarceloFantini » Sex Abr 15, 2011 20:09
por MarceloFantini » Sex Abr 15, 2011 20:09
Suponha que

é par. Logo,
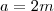
para

inteiro. Segue que

, com

inteiro. Absurdo, pois nossa hipótese é de que

é ímpar. Então,
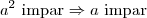
.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Sáb Abr 16, 2011 12:19
por Abelardo » Sáb Abr 16, 2011 12:19
Fantini, poderia demonstrar dessa maneira? Por favor, aponte os erros e, se possível, indique algum livro ou arquivo que trate sobre essas questões de demonstração. Sei que existem algumas técnicas, mas não consigo nem encontrar nas livrarias algum que trate do assunto (É claro, no nível de um aluno do ensino médio).

não divide
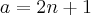
nos inteiros (Acho que não é dessa forma que se diz, mas vai lá). Sendo
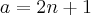
, então


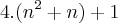
não é divisível por 2. Se a^2 não é divisível por 2 será um número ímpar.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Abr 16, 2011 15:21
por MarceloFantini » Sáb Abr 16, 2011 15:21
Mas o que eu fiz foi a demonstração. Sobre a sua: se 2 não divide
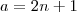
, então

não é par, e portanto

é ímpar, que é a sua TESE, logo está errado pois você partiu do que você queria provar. Na verdade você fez foi a demonstração de que se

é ímpar então

é ímpar.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Abelardo » Sáb Abr 16, 2011 15:47
por Abelardo » Sáb Abr 16, 2011 15:47
Fantini, ''eu'' poderia demonstrar dessa maneira? Por favor, apo...
Há algum material que fale sobre esse tipo de questão? Obrigado pelas correções, vi alguns artigos no wikipedia, mas não entendi bem as diferenças de tese, hipótese, corolário ... nomenclatura confusa.
-

Abelardo
- Colaborador Voluntário

-
- Mensagens: 159
- Registrado em: Qui Mar 03, 2011 01:45
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Sáb Abr 16, 2011 15:56
por MarceloFantini » Sáb Abr 16, 2011 15:56
Demonstrar da maneira que fiz, sim. Do jeito que você fez, não (não para o que você queria provar). Não conheço muito material em específico falando sobre isso, mas procure livros sobre demonstrações. Em inglês há vários. Sobre a nomenclatura, o básico é:
Teorema: afirmação a ser demonstrada.
Hipótese: o que vocÊ assume como verdade.
Tese: o que você quer provar (e portanto não sabe se é verdade ainda).
Colorário/lema: outro nome para teorema, só que de demonstração mais imediata/tese mais fraca.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo para Funções de Uma Variável Real I
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3213 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
-
- Provar que ||u|| > 0
por 0 kelvin » Qui Mar 24, 2011 20:35
- 2 Respostas
- 1971 Exibições
- Última mensagem por 0 kelvin

Qui Mar 24, 2011 21:16
Geometria Analítica
-
- provar que
por anamendes » Ter Jun 19, 2012 07:41
- 1 Respostas
- 1419 Exibições
- Última mensagem por fraol

Qua Jun 20, 2012 21:19
Trigonometria
-
- Provar
por Jovani Souza » Ter Jun 11, 2013 21:03
- 0 Respostas
- 1018 Exibições
- Última mensagem por Jovani Souza

Ter Jun 11, 2013 21:03
Álgebra Elementar
-
- provar!
por Jovani Souza » Qua Jul 03, 2013 18:27
- 0 Respostas
- 1174 Exibições
- Última mensagem por Jovani Souza

Qua Jul 03, 2013 18:27
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
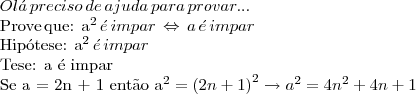

 é ímpar, então
é ímpar, então  para algum k natural.
para algum k natural. .
.
 par e veja uma contradição.
par e veja uma contradição.


 é par. Logo,
é par. Logo, 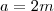 para
para  inteiro. Segue que
inteiro. Segue que  , com
, com  inteiro. Absurdo, pois nossa hipótese é de que
inteiro. Absurdo, pois nossa hipótese é de que  é ímpar. Então,
é ímpar. Então, 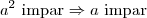 .
.

 não divide
não divide 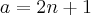 nos inteiros (Acho que não é dessa forma que se diz, mas vai lá). Sendo
nos inteiros (Acho que não é dessa forma que se diz, mas vai lá). Sendo 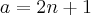 , então
, então 

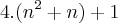 não é divisível por 2. Se a^2 não é divisível por 2 será um número ímpar.
não é divisível por 2. Se a^2 não é divisível por 2 será um número ímpar.
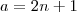 , então
, então  não é par, e portanto
não é par, e portanto  é ímpar, que é a sua TESE, logo está errado pois você partiu do que você queria provar. Na verdade você fez foi a demonstração de que se
é ímpar, que é a sua TESE, logo está errado pois você partiu do que você queria provar. Na verdade você fez foi a demonstração de que se  é ímpar então
é ímpar então  é ímpar.
é ímpar.




