Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por stalone » Sex Dez 18, 2009 17:38
por stalone » Sex Dez 18, 2009 17:38
O problema é o seguinte :
Uma mãe é 21 anos mais velha que o filho.
Daqui a seis anos o filho terá uma idade 5 vezes menor que a da mãe.
Pergunta: Onde está o pai agora ?
Atenção à pergunta: Onde está o pai agora?
-
stalone
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Dez 18, 2009 16:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Computação
- Andamento: formado
 por Molina » Sáb Dez 19, 2009 13:43
por Molina » Sáb Dez 19, 2009 13:43
Problema tradicional da matemática.
Muito legal e de fato matematicamente resolvivel!
Vou deixar mais um tempo para o pessoal que desconhece tentar.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Cleyson007 » Seg Dez 21, 2009 22:29
por Cleyson007 » Seg Dez 21, 2009 22:29
Boa noite!
O problema é muito interessante!
Vamos montar as equações do problema:
Idade atual da mãe: x anos
Idade atual do menino: y anos
Como a mãe é 21 anos mais velha que o filho:
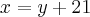
Passados os 06 anos:

e

Como a mãe é 5 vezes mais velha que o filho:
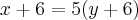
Resolvendo o sistema de equações:
Idade da criança:

anos
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10712 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9716 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3309 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4601 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6525 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





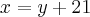
 e
e 
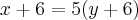
 anos
anos



 .
.



