DESAFIO PARA OS CRÂNIOS DA MATEMÁTICA

por **tenebroso** » Qua Dez 18, 2013 17:46

1) OBSERVE O ESQUEMA ABAIXO, LEMBRANDO QUE, AS ALTURAS DOS ALUNOS DE UMA TURMA É COMPOSTA POR 50 ESTUDANTES.

ALTURA: 1,56; FREQUÊNCIA 12.
ALTURA: 1,68; FREQUÊNCIA 10.
ALTURA: 1,75; FREQUÊNCIA 8.
ALTURA: 1,80; FREQUÊNCIA 10.
ALTURA: 1,85; FREQUÊNCIA 10.

CHAMANDO Ma, A MÉDIA ARITMÉTICA DAS ALTURAS; Me, A MEDIANA DAS ALTURAS E Mo, A MODA DAS ALTURAS, PODE-SE AFIRMAR QUE:

A) Mo menor que Ma menor que Me
B) Me menor que Mo menor que Ma
c) Me menor que Ma menor que Mo
D) Mo menor que Me menor que Ma
E) Ma menor que Me menor que Mo

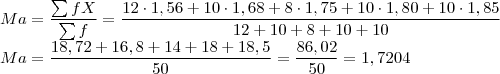
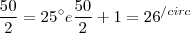
por **Baltuilhe** » Seg Abr 06, 2015 19:10

Boa tarde!

Calculando a média (Ma):
$\\Ma=\frac{\sum{fX}}{\sum{f}}=\frac{12\cdot 1,56+10\cdot 1,68+8\cdot 1,75+10\cdot 1,80+10\cdot 1,85}{12+10+8+10+10}\\ Ma=\frac{18,72+16,8+14+18+18,5}{50}=\frac{86,02}{50}=1,7204$

Calculando a mediana (Me):
Como temos 50 números temos dois termos medianos. A posição deles vale: ${\frac{50}{2}}=25^{\circ} e {\frac{50}{2}}+1=26^{/circ}$
Temos 12 temos, mais 10, 22, mais 8, 30. Ou seja, os dois termos medianos valem 1,75, então, a mediana TAMBÉM valerá 1,75.

Calculando a moda(Mo):
A moda é o termo com maior frequência (moda bruta)
Então, moda (Mo) = 1,56

Temos, então:
Mo < Ma < Me (letra a)

DESAFIO PARA OS CRÂNIOS DA MATEMÁTICA

DESAFIO PARA OS CRÂNIOS DA MATEMÁTICA

DESAFIO PARA OS CRÂNIOS DA MATEMÁTICA

Re: DESAFIO PARA OS CRÂNIOS DA MATEMÁTICA

Quem está online