Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por tenebroso » Qua Dez 18, 2013 17:46
por tenebroso » Qua Dez 18, 2013 17:46

1) OBSERVE O ESQUEMA ABAIXO, LEMBRANDO QUE, AS ALTURAS DOS ALUNOS DE UMA TURMA É COMPOSTA POR 50 ESTUDANTES.
ALTURA: 1,56; FREQUÊNCIA 12.
ALTURA: 1,68; FREQUÊNCIA 10.
ALTURA: 1,75; FREQUÊNCIA 8.
ALTURA: 1,80; FREQUÊNCIA 10.
ALTURA: 1,85; FREQUÊNCIA 10.
CHAMANDO Ma, A MÉDIA ARITMÉTICA DAS ALTURAS; Me, A MEDIANA DAS ALTURAS E Mo, A MODA DAS ALTURAS, PODE-SE AFIRMAR QUE:
A) Mo menor que Ma menor que Me
B) Me menor que Mo menor que Ma
c) Me menor que Ma menor que Mo
D) Mo menor que Me menor que Ma
E) Ma menor que Me menor que Mo
-
tenebroso
- Usuário Ativo

-
- Mensagens: 15
- Registrado em: Qua Dez 18, 2013 16:00
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: estudante
- Andamento: cursando
 por Baltuilhe » Seg Abr 06, 2015 19:10
por Baltuilhe » Seg Abr 06, 2015 19:10
Boa tarde!
Calculando a média (Ma):
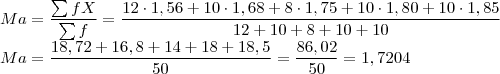
Calculando a mediana (Me):
Como temos 50 números temos dois termos medianos. A posição deles vale:
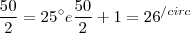
Temos 12 temos, mais 10, 22, mais 8, 30. Ou seja, os dois termos medianos valem 1,75, então, a mediana TAMBÉM valerá 1,75.
Calculando a moda(Mo):
A moda é o termo com maior frequência (moda bruta)
Então, moda (Mo) = 1,56
Temos, então:
Mo < Ma < Me (letra a)
-
Baltuilhe
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Dom Mar 24, 2013 21:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: formado
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desafio para determinar a data de entrega
por Eekhoorn » Qui Mar 05, 2009 12:35
- 2 Respostas
- 3912 Exibições
- Última mensagem por m0x0

Sáb Jul 23, 2011 17:41
Desafios Enviados
-
- Desafio Fácil para vocêis me ajudarem
por Jonatasskylinknot » Qui Fev 24, 2011 20:54
- 1 Respostas
- 3614 Exibições
- Última mensagem por Abelardo

Seg Mar 07, 2011 03:42
Desafios Fáceis
-
- [Matematica Financeira] Questão desafio
por CARLOS POVOAS » Qua Jun 19, 2013 00:35
- 0 Respostas
- 1787 Exibições
- Última mensagem por CARLOS POVOAS

Qua Jun 19, 2013 00:35
Matemática Financeira
-
- Livro: Matematica basica para ensino fundamental. pg. 55 ex1
 por santiago alves » Sex Jul 08, 2011 08:46
por santiago alves » Sex Jul 08, 2011 08:46
- 2 Respostas
- 2890 Exibições
- Última mensagem por santiago alves

Sex Jul 08, 2011 10:46
Polinômios
-
- Livro: Matematica basica para ensino Superior. pg. 59 ex4
por santiago alves » Ter Jul 12, 2011 13:45
- 2 Respostas
- 2374 Exibições
- Última mensagem por santiago alves

Ter Jul 12, 2011 14:23
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


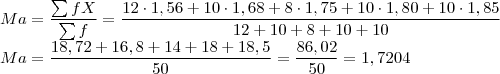
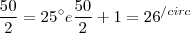



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.