Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Dom Mai 03, 2009 06:07
por Molina » Dom Mai 03, 2009 06:07
Qual o próximo número da sequència:
1, 2, 3, 4, 5, 8, 7, 16, 9 ... 
Good luck!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rafagondi » Ter Mai 05, 2009 22:14
por rafagondi » Ter Mai 05, 2009 22:14
Ahá!!
Demorei uns 15 minutos olhando essa seqüência! Mas acho que valeu a pena!
Lá vai os números que eu acho que continuam a seqüência:
1, 2, 3, 4, 5, 8, 7, 16, 9 ... 32, 11, 64, 13 ...
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por lucasguedes » Ter Jul 07, 2009 15:20
por lucasguedes » Ter Jul 07, 2009 15:20
rafagondi escreveu:Ahá!!
Demorei uns 15 minutos olhando essa seqüência! Mas acho que valeu a pena!
Lá vai os números que eu acho que continuam a seqüência:
1, 2, 3, 4, 5, 8, 7, 16, 9 ... 32, 11, 64, 13 ...
coloca a formula de sua resposta (como vc fez)
a minha foi essa: 1, 2¹, 3, 2², 5, 2³, 7,
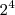
, 9,

...

= 32
-
lucasguedes
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jun 25, 2009 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso tecnico em eletrotecnica
- Andamento: cursando
 por rafagondi » Ter Jul 07, 2009 20:49
por rafagondi » Ter Jul 07, 2009 20:49
A forma como eu fiz foi a seguinte:
Eu percebi que os números intercalam entre os ímpares e as potências de 2.
Da seguinte forma:
(1°ímpar), 2¹, (2° ímpar), 2², (3° ímpar), 2³, (4° ímpar) ... e assim sucessivamente.
Espero estar certo.
________________________________________________
Rafael Agondi - Física/Matemática Bacharelado UNICAMP
-

rafagondi
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Abr 23, 2009 21:18
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Física Licenciatura - UNICAMP
- Andamento: cursando
 por lucasguedes » Ter Jul 07, 2009 21:08
por lucasguedes » Ter Jul 07, 2009 21:08
rafagondi escreveu:A forma como eu fiz foi a seguinte:
Eu percebi que os números intercalam entre os ímpares e as potências de 2.
Da seguinte forma:
(1°ímpar), 2¹, (2° ímpar), 2², (3° ímpar), 2³, (4° ímpar) ... e assim sucessivamente.
Espero estar certo.
Certíssimo!! =D
-
lucasguedes
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qui Jun 25, 2009 19:12
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: curso tecnico em eletrotecnica
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [sequencia] Calcular limite de sequencia por definição
 por amigao » Ter Abr 15, 2014 15:15
por amigao » Ter Abr 15, 2014 15:15
- 4 Respostas
- 3997 Exibições
- Última mensagem por e8group

Dom Mai 11, 2014 17:09
Sequências
-
- MAIS UMA QUESTÃO DE G.A
por GABRIELA » Ter Set 29, 2009 18:57
- 3 Respostas
- 2541 Exibições
- Última mensagem por Elcioschin

Qua Set 30, 2009 20:54
Geometria Analítica
-
- Mais uma questão
por GABRIELA » Seg Dez 07, 2009 17:16
- 1 Respostas
- 2188 Exibições
- Última mensagem por Elcioschin

Seg Dez 07, 2009 19:23
Estatística
-
- Mais um desafio..
por victoreis1 » Seg Nov 22, 2010 21:26
- 3 Respostas
- 2520 Exibições
- Última mensagem por Molina

Seg Nov 22, 2010 23:54
Desafios Difíceis
-
- Mais uma questão de log
por my2009 » Qua Jan 26, 2011 11:41
- 1 Respostas
- 1398 Exibições
- Última mensagem por Molina

Qua Jan 26, 2011 15:21
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 Good luck!
Good luck! 

 Good luck!
Good luck! 


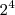 , 9,
, 9,  ...
... = 32
= 32

