fraol escreveu:De fato, como o professor demonstrou,
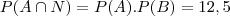
que é diferente de 0.
Com isso a probabilidade de que uma bola retirada seja Amarela e tenha o número 1 é de 12,5%.
Por outro lado se tivermos, por exemplo oito bolas no saco, quatro serão amarelas (50%) , digamos que numeradas de 2 a 5, e duas terão o número 1 (25%), digamos que seja uma verde e outra branca.
Eu havia pensado um pouco nesse problema e acho não há como provar propriamente o que foi pedido.
O que vocês acham?
O seu raciocínio tem um furo. Qual é a probabilidade da bola retirada ser amarela ou ter o número 1?
Você tem que armar um exemplo na qual essa probabilidade seja 62,5% (como informa no exercício), mas sem que haja a bola amarela de número 1.
No exemplo que você deu, temos que:
-- 4 bolas amarelas: com números de 2 até 5;
-- 1 bola verde: com o número 1;
-- 1 bola branca: com o número 1;
Você ainda precisa completar esse exemplo informando mais 2 bolas (já que o seu total era de 8). Agora tente completar de modo que aquela última probabilidade seja 62,5%, mas sem que haja a bola amarela de número 1.




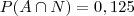

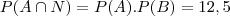 que é diferente de 0.
que é diferente de 0. , do saco de oito bolas deveria ser de bolas amarelas e com o número 1. Ou seja uma bola. Então está provado.
, do saco de oito bolas deveria ser de bolas amarelas e com o número 1. Ou seja uma bola. Então está provado.