Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por admin » Sáb Jul 21, 2007 01:18
por admin » Sáb Jul 21, 2007 01:18
Três pessoas chegaram ao Hotel Nelson e ao todo pagaram 30 dólares por um quarto. Mais tarde, o gerente descobriu haver cometido um engano e que os hóspedes tinham pago a mais. Mandou então o mensageiro devolver-lhes 5 dólares. No caminho, o mensageiro decidiu se apropriar da sua gorgeta (para ter certeza de recebê-la) e reteve 2 dólares para si, devolvendo apenas 3 aos hóspedes. Assim, cada hóspede pagou apenas 9 dólares pelo quarto, ficando o mensageiro com 2. Isso perfaz um total de 27 + 2 = 29. O que aconteceu ao outro dólar?
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Skambha » Qui Fev 05, 2009 21:24
por Skambha » Qui Fev 05, 2009 21:24
Eaw , bom veja se estou certo se teriam que pagar 30 dolares mas eles pagaram a mais e foi devolvido 5 entao quer dizer que eles pagaram 35 ou seja esse 1 dolar nao foi perdido estou certo?
-

Skambha
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Fev 05, 2009 21:20
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Seg Fev 09, 2009 10:45
por Neperiano » Seg Fev 09, 2009 10:45
Ola
Creio que naum esteja certo Skambha
Bom eu naum sei aonde foi o outro dólar, mas se eu achar eh meu.
Realmente eu não sei então por isso vou chutar.
Pode ser que esse dólar seja do gerente.
Ou pode ser que o dólar ficou com o Nélson.
Acredito mais na primeira Hipótese.
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por [++] » Qui Jul 16, 2009 15:02
por [++] » Qui Jul 16, 2009 15:02
fabiosousa escreveu:Três pessoas chegaram ao Hotel Nelson e ao todo pagaram 30 dólares por um quarto. Mais tarde, o gerente descobriu haver cometido um engano e que os hóspedes tinham pago a mais. Mandou então o mensageiro devolver-lhes 5 dólares. No caminho, o mensageiro decidiu se apropriar da sua gorgeta (para ter certeza de recebê-la) e reteve 2 dólares para si, devolvendo apenas 3 aos hóspedes. Assim, cada hóspede pagou apenas 9 dólares pelo quarto, ficando o mensageiro com 2. Isso perfaz um total de 27 + 2 = 29. O que aconteceu ao outro dólar?
então ao todo, eles teriam q pagar 25 dólares, e não trinta, então o gerente devolveu 5, o mensageiro pegou 2 dólares para si, então deu 3 dólares aos clientes, mas como a pergunta é : "O QUE ACONTECEU AO OUTRO DÓLAR?" respondo: não se deve somar os 2 dólares aos 27, e sim retirar os dois dólares, pois os três hospedes iam dar (ou não) os dois dólares , sendo assim : 27 - 2 = 25>>o valor total do aluguel do quarto
espero ter ajudado,
blz??
-
[++]
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Jul 15, 2009 23:55
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Cleyson007 » Qui Jul 16, 2009 17:43
por Cleyson007 » Qui Jul 16, 2009 17:43
Boa tarde!
Deixa que respondo essa

Valor cobrado:
30 dólaresComo são 03 pessoas, o valor que ficou para cada um pagar:
30/3 = 8,3333333333Valor devolvido aos hóspedes: 03 dólares --> Ou seja:
9,3333333333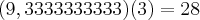
Como o mensageiro apropriou da gorgeta de 2 dólares:
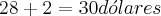
O problema é interessante

Até mais.
Abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por [++] » Sex Jul 17, 2009 21:56
por [++] » Sex Jul 17, 2009 21:56
Cleyson007 , não entendi seu raciocínio... afinal, o que os tres hospedes pagariam era 25 dolares, não 30, não entendi... explica?
-
[++]
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Qua Jul 15, 2009 23:55
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
 por Molina » Sex Jul 17, 2009 22:15
por Molina » Sex Jul 17, 2009 22:15
Pegadinha clássica de matemática, onde todos são induzidos a pensar de um modo, só que na verdade trata-se de um problema simples:
Dos
30 reais dados,
25 reais ficaram com dono do hotel,
3 reais foram devolvidos para os hóspedes e
2 reais ficou com o mensageiro.
25 + 3 + 2 = 30.
A grande pegadinha dessa questão, é o final dela:
Assim, cada hóspede pagou apenas 9 dólares pelo quarto, ficando o mensageiro com 2. Isso perfaz um total de 27 + 2 = 29. O que aconteceu ao outro dólar? que nos induz a pensar de outra forma.
Espero ter ajudado com quem estava com dúvidas.
Podemos debater mais sobre o assunto.
Abraços,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Desafios Médios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.














 , avisa que eu resolvo.
, avisa que eu resolvo.

