Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por alexandre32100 » Qui Ago 19, 2010 14:53
por alexandre32100 » Qui Ago 19, 2010 14:53
"Todo número negativo é ímpar."Para provar a afirmativa, começarei admitindo que há um número negativo par e então, chegarei a um absurdo.
Tome o menor número par negativo e chame-o de

. Logicamente, o número

é par e menor que

(deve-se lembrar que está se lidando com número negativos!). Um absurdo, afinal foi definido inicialmente que

é o menor par negativo.

Onde está a "trapaça" desta prova?
-
alexandre32100
-
 por Elcioschin » Qui Ago 19, 2010 17:57
por Elcioschin » Qui Ago 19, 2010 17:57
O absurdo é a frase:
Tome o MENOR número par negativo ----> Este número deve supostamente ser - 2
Acontece que este número é o MAIOR número par negativo. Por exemplo - 2 > - 4
Isto acontece porque, para os negativos, quanto MAIOR o módulo do número, MENOR o valor do número
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por Molina » Qui Ago 19, 2010 22:10
por Molina » Qui Ago 19, 2010 22:10
Boa noite, Alexandre.
Pra mim o erro está em assumir que

é o menor negativo par, pois o absurdo que você chega contraria isso.
Caso sua questão fosse verdade, poderia escrever uma deste tipo:
"Todo número negativo é par."
Para provar a afirmativa, começarei admitindo que há um número negativo ímpar e então, chegarei a um absurdo.
Tome o menor número ímpar negativo e chame-o de  . Logicamente, o número
. Logicamente, o número  é ímpar e menor que
é ímpar e menor que  (deve-se lembrar que está se lidando com número negativos!). Um absurdo, afinal foi definido inicialmente que
(deve-se lembrar que está se lidando com número negativos!). Um absurdo, afinal foi definido inicialmente que  é o menor ímpar negativo.
é o menor ímpar negativo.Logo pela sua questão
Nenhum número negativo é par e pela minha
Nenhum número negativo é ímpar. Afinal, o que então são os negativos?
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por paulo87 » Sáb Fev 19, 2011 12:15
por paulo87 » Sáb Fev 19, 2011 12:15
molina, so um obs.. eh q nem todo numero multiplicado por 3 é impar... e eu acho q essa afirmação é errada, pois foi adotada uma definição errada de infinito.
-
paulo87
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Fev 19, 2011 12:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Sáb Fev 19, 2011 13:34
por LuizAquino » Sáb Fev 19, 2011 13:34
alexandre32100 escreveu:Onde está a "trapaça" desta prova?
A "trapaça" está em admitir que o conjunto
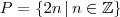
possui um menor elemento, o que é falso. O conjunto
P é ilimitado, assim como

.
paulo87 escreveu:molina, so um obs.. eh q nem todo numero multiplicado por 3 é impar...
Note que o Molina assumiu que b é ímpar, portanto 3b é ímpar também. O triplo de todo número ímpar também é ímpar.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Potenciação] raiz de número negativo,sendo tudo ao quadrado
por Debora Bruna » Sex Jun 26, 2015 23:02
- 3 Respostas
- 2683 Exibições
- Última mensagem por DanielFerreira

Dom Jun 28, 2015 16:01
Álgebra Elementar
-
- parte-todo
por leticiapires52 » Sex Ago 15, 2014 13:23
- 0 Respostas
- 1665 Exibições
- Última mensagem por leticiapires52

Sex Ago 15, 2014 13:23
Números Complexos
-
- MDE NEGATIVO
por laura1970 » Sex Fev 22, 2013 19:46
- 0 Respostas
- 1183 Exibições
- Última mensagem por laura1970

Sex Fev 22, 2013 19:46
Aritmética
-
- Questão de concurso- Parte/Todo
por Pri Ferreira » Qua Mar 21, 2012 14:01
- 1 Respostas
- 1780 Exibições
- Última mensagem por LuizAquino

Qua Mar 21, 2012 20:50
Álgebra Elementar
-
- Prove para todo n natural
por Cleyson007 » Sáb Abr 28, 2012 17:14
- 4 Respostas
- 2367 Exibições
- Última mensagem por Cleyson007

Sáb Abr 28, 2012 18:23
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Logicamente, o número
. Logicamente, o número  é par e menor que
é par e menor que  (deve-se lembrar que está se lidando com número negativos!). Um absurdo, afinal foi definido inicialmente que
(deve-se lembrar que está se lidando com número negativos!). Um absurdo, afinal foi definido inicialmente que  é o menor par negativo.
é o menor par negativo. 


 . Logicamente, o número
. Logicamente, o número  é ímpar e menor que
é ímpar e menor que 

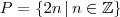 possui um menor elemento, o que é falso. O conjunto
possui um menor elemento, o que é falso. O conjunto  .
.![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.