"Considere três lotes de 20 peças cada. O número de peças dentro do padrão no primeiro, segundo e terceiro lote são, respectivamente, 20, 15 e 10. De um lote escolhido ao acaso, retira-se uma peça aleatoriamente e verifica-se que está dentro do padrão. Devolve-se a peça ao lote e efetua-se uma nova retirada do mesmo lote e verifica-se que a segunda peça também está dentro do padrão.
a) Qual a probabilidade das duas peças retiradas estarem dentro do padrão?
b)Qual a probabilidade das peças terem sido retiradas do terceiro lote? "
Tenho aqui a solução que foi apresentada, contudo não entendi o que foi realizado:
a)
P(P1) = 1; P(P2) = 3/4; P(P3) = 1/2

P = 29/48
Não entendi qual lógica que ele está usando com esses termos ao quadrado, qual fórmula!
Consequentemente não entendi a b)
b)
P(P|3° lote) = 1/4
P(P|2° lote) = 9/16
P(P|1° lote) = 1
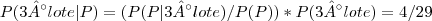
Agradeceria se alguém pudesse me ajudar a entender




 .
.
 :
: