Ana Maria,
de acordo com a condição de existência de um triângulo, a medida de qualquer um dos lados é menor que a soma dos outros dois, e, maior que o valor absoluto da diferença entre eles. Com isso, consideremos o outro lado como

, temos então:
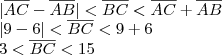
Logo, teremos as seguintes possibilidades para que o triângulo exista: 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 e 14.
Resultando
13 possibilidades!!



 , temos então:
, temos então: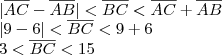




 .
.



