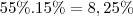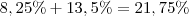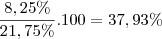por probestat » Sáb Dez 01, 2012 16:46
por probestat » Sáb Dez 01, 2012 16:46
Duvida sobre teorema de Bayes
Pessoal, poderiam me ajudar? Estou com uma questão sobre o teorema de Bayes conforme enunciado abaixo, cheguei no valor de 15,9 mais não bateu com a resposta. Estou com duvida, pois o enunciado informa PR mais o teorema informa PA. Será que alguém poderia dar uma ajuda?
Segue abaixo:
Pergunta - Dois agricultores fornecem verduras para um supermercado. O agricultor R fornece 55% das verduras e o agricultor T 45%.
Sabe-se que 15% das verduras são fornecidas por R e 30% por T são alface. Qual a probabilidade de um pé de alface, escolhido ao acaso, ter vindo do fornecedor R?
Para facilitar o raciocínio, utilize a nomenclatura sugerida abaixo:
P(R) = Probabilidade de a verdura ter vindo do fornecedor R = 55%
P(T) = Probabilidade de a verdura ter vindo do fornecedor T = 45%
P(R/A) = Probabilidade de a verdura ter vindo do fornecedor R, sabendo que é alface = 30%
P(A/R) = Probabilidade de ser alface, sabendo que veio do fornecedor R =
P(A/T) = Probabilidade de ser alface, sabendo que veio do fornecedor T =
-
probestat
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Dez 01, 2012 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
 por young_jedi » Sáb Dez 01, 2012 17:54
por young_jedi » Sáb Dez 01, 2012 17:54
vamos achar a porcentagem do total de verduras que são alfaces vindas de R
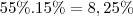
vamos achar a porcentagem do total de verduras que são alfaces vindas de T

vamos achar a porcentagem do total que são alface
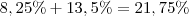
aogra vamos achar a porcentagem de alface vindas de R
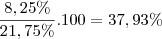
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por probestat » Sáb Dez 01, 2012 19:24
por probestat » Sáb Dez 01, 2012 19:24
young_jedi escreveu:vamos achar a porcentagem do total de verduras que são alfaces vindas de R
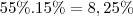
vamos achar a porcentagem do total de verduras que são alfaces vindas de T

vamos achar a porcentagem do total que são alface
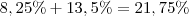
aogra vamos achar a porcentagem de alface vindas de R
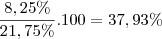
Perfeito, agora entendi como fazer o calculo, obrigado!!!
-
probestat
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Dez 01, 2012 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: cursando
Voltar para Probabilidade
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema de Bayes
por martin34 » Sáb Abr 02, 2011 18:03
- 0 Respostas
- 1877 Exibições
- Última mensagem por martin34

Sáb Abr 02, 2011 18:03
Estatística
-
- Teorema de Bayes
por probestat » Sáb Dez 01, 2012 18:15
- 3 Respostas
- 2199 Exibições
- Última mensagem por Fabio Wanderley

Ter Dez 18, 2012 00:47
Probabilidade
-
- Probabilidade - Teorema de Bayes
por sergiomk86 » Qua Dez 22, 2010 19:17
- 2 Respostas
- 2878 Exibições
- Última mensagem por junedm

Ter Set 24, 2013 16:07
Estatística
-
- Probabilidade -Bayes
por benni » Qui Mai 19, 2011 15:50
- 2 Respostas
- 2492 Exibições
- Última mensagem por arima

Seg Mai 23, 2011 21:22
Estatística
-
- Teorema das linhas
por valleska » Seg Mai 18, 2009 21:46
- 1 Respostas
- 3258 Exibições
- Última mensagem por Guill

Dom Jul 10, 2011 11:20
Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.