 por Victor Gabriel » Dom Mai 05, 2013 08:27
por Victor Gabriel » Dom Mai 05, 2013 08:27
Olá, gostaria que alguém mim explica-se esta questão, ficarei muito grato!
Questão: O código de Morse usa duas letras, traços e ponto, e as palavras tem de 1 a 4 letras. Quantas são as palavras do código de Morse?
-
Victor Gabriel
- Usuário Dedicado

-
- Mensagens: 48
- Registrado em: Dom Abr 14, 2013 20:29
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: estudante
- Andamento: cursando
 por Luis Gustavo » Seg Mai 06, 2013 16:13
por Luis Gustavo » Seg Mai 06, 2013 16:13
Bom, esse enunciado tá meio errado. O que código morse usa não são duas letras, mas sim dois símbolos, ponto e traço, para representar as letras, e as "palavras" formadas podem sim ter mais de quatro símbolos, acho que chegam até seis, se não me engano. Mas vou dar a resposta de acordo com o enunciado que você postou.
As palavras formadas podem ter uma, duas, três ou quatro letras. Vamos contar quantas palavras com cada quantidade de letras existem e depois somá-las.
- Palavras de uma letra
Só existem duas palavras com uma letra, já que só existem duas letras.
- Palavras de duas letras
Para a primeira letra, são duas possibilidades: ponto e traço. Para a segunda letra, também são duas possibilidades. Logo, o número de palavras com duas letras é:
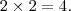
- Palavras de três letras
Duas possibilidades para a primeira letra, duas para a segunda letra e duas novamente para a terceira. O número de palavras com três letras é:

- Palavras de quatro letras
Duas possibilidades para a primeira letra, duas para a segunda, duas para a terceira e duas para a quarta. O número total de palavras com quatro letras é:
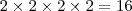
Somando todas as palavras, temos o número total de palavras no código morse, que é:
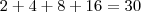 Resposta:
Resposta: São 30 as palavras do código morse.
Espero ter ajudado.
Att, Luis Gustavo.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Análise Combinatória
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Combinatória-analise combinatoria
por heloisacarvalho83 » Seg Fev 27, 2012 22:40
- 1 Respostas
- 2880 Exibições
- Última mensagem por Livia000

Qua Mai 23, 2012 00:26
Estatística
-
- combinatória
por Adilson » Sex Ago 28, 2009 13:50
- 1 Respostas
- 2133 Exibições
- Última mensagem por Molina

Sex Ago 28, 2009 21:19
Estatística
-
- Combinatória
por 2137RF » Sex Out 09, 2009 11:25
- 4 Respostas
- 3464 Exibições
- Última mensagem por shirata

Qui Nov 26, 2009 06:38
Estatística
-
- combinatória
por apoliveirarj » Dom Jul 25, 2010 16:50
- 2 Respostas
- 4869 Exibições
- Última mensagem por apoliveirarj

Qui Ago 05, 2010 19:27
Estatística
-
- Combinatória
por apoliveirarj » Sáb Ago 07, 2010 12:23
- 2 Respostas
- 2460 Exibições
- Última mensagem por apoliveirarj

Sex Ago 13, 2010 15:55
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 , avisa que eu resolvo.
, avisa que eu resolvo.

