Não consigo fazer esses exercicios, alguém me ajuda?
Se não são permitidas repetições e utilizando somente os algarismos 0,1,2,3,4,5,6:
a) quantos números de 4 algarismos podemos formar?
b) quantos desses números de 4 algarismos são pares?
b) quantos desses números de 4 algarismos são maiores que 2000?
Com os algarismos 1,2,3,4,5 e 6, quanto s números de 3 algarismos distintos menores que 400 podemos formar?
Um colegiado de 5 membros será selecionado dentre 12 candidatos a membros titulares e 8 candidatos a membros suplentes. De quantas maneiras isso pode ser feito se o colegiado deve consistir
b) de pelo menos 2 titulares e 1 suplente?







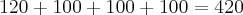 números pares.
números pares. números maiores que 2000.
números maiores que 2000.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)