 por Debora Bruna » Seg Jan 11, 2016 18:48
por Debora Bruna » Seg Jan 11, 2016 18:48
Quando li esse exercício,((UFSM-RS) Acrescentando-se dois novos elementos a um conjunto A, verificou-se que o número de subconjuntos de A teve um acréscimo de 384. Quantos elementos possuía originalmente o conjunto A?) comecei da seguinte forma:
Acrescentando-se dois novos elementos a um conjunto A
Conjunto A = n, acrescentando-se 2, vai n+2.
o número de subconjuntos de A teve um acréscimo de 384
n=2^n. e n+2= 2^n+2
começando a resolver:
n+2= 2^n+2 + 384.
Parei aqui.
A resolução que encontrei na internet é essa:
2n+2 = 2n+384
2n. 2^2 = 2n + 384
4. 2n= 2n+384
2n= 384/3
2n=128
2n= 2^7
n=7
E depois de torrar todos os neurônios, a entendi. Só que porque não começa com: ? Já que, se o número de elementos de um conjunto n = 2^n, então o número de elementos de um conjunto n+2 = 2^n+2, então deveria prosseguir da seguinte forma n+2= 2^n+2 + 384, não é?
-
Debora Bruna
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Dez 15, 2014 17:49
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por DanielFerreira » Dom Fev 07, 2016 15:05
por DanielFerreira » Dom Fev 07, 2016 15:05
Debora Bruna escreveu:(UFSM-RS) Acrescentando-se dois novos elementos a um conjunto A, verificou-se que o número de subconjuntos de A teve um acréscimo de 384. Quantos elementos possuía originalmente o conjunto A?
Vamos supor que o conjunto A tenha

elementos, então a quantidade de subconjuntos do conjunto A é dado por
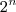
.
Ora, se acrescentamos dois elementos ao conjunto A, podemos concluir que o número de subconjuntos do "novo" conjunto será dado por
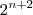
.
Do enunciado,

"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Conjuntos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em exercicio de Conjuntos
por krobc » Sáb Mar 17, 2012 12:07
- 0 Respostas
- 1176 Exibições
- Última mensagem por krobc

Sáb Mar 17, 2012 12:07
Conjuntos
-
- [Conjuntos] Dúvida em exercício.
por Debora Bruna » Seg Jan 11, 2016 18:49
- 1 Respostas
- 2117 Exibições
- Última mensagem por DanielFerreira

Dom Fev 07, 2016 20:49
Conjuntos
-
- [Conjuntos] Exercício de conjuntos com áreas
 por redleader » Ter Abr 02, 2013 16:12
por redleader » Ter Abr 02, 2013 16:12
- 0 Respostas
- 1543 Exibições
- Última mensagem por redleader

Ter Abr 02, 2013 16:12
Conjuntos
-
- [Conjuntos] Dúvida sobre conjuntos vazios
por ALPC » Qui Set 18, 2014 18:28
- 5 Respostas
- 6396 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 15:44
Conjuntos
-
- Exercício de Conjuntos
por Loretto » Seg Out 11, 2010 18:26
- 0 Respostas
- 1312 Exibições
- Última mensagem por Loretto

Seg Out 11, 2010 18:26
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 elementos, então a quantidade de subconjuntos do conjunto A é dado por
elementos, então a quantidade de subconjuntos do conjunto A é dado por 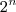 .
.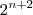 .
.
