Conjunto Vazio
![F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]]](/latexrender/pictures/d4f2e795300c9fede3b8aa3f370ca35a.png "F = \left[\,x \,| \,x \,\in \, $\mathbb{Z}$ \, e \:x^2 \:+ 1 \,= \,\,0\right]]")
pelo que eu entendi, ele está dizendo que para o x pertencer ao conjunto F, é preciso que ele pertença aos números inteiros e que ao ser elevado ao quadrado e ser somado com 1 fique 0.
Pela minha interpretação, ao falar que esse conjunto é vazio, não existe nenhum número que ao passar pelos procedimentos acima se torne 0. Mas então eu pensei:
-1 pertence aos números inteiros então:
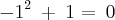
o livro que está errado ou é meu raciocínio ?
![\\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...)](/latexrender/pictures/82511f06534b2299cd66c79bee546db2.png "\\ x^2 + 1 = 0 \\\\ x^2 = - 1 \\\\ x = \sqrt[2]{- 1} \\\\ (...)")
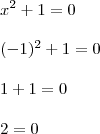
,eita num sei usar esse editor,mas e isso num tem xao quadradop ,mais yao quadrado mais um igual a zero,nao existe sol.real...deu pra entender...
por ![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)