![A= ]-\infty;8] A= ]-\infty;8]](/latexrender/pictures/c6361ee25c15154ca65b2dc703e7c2cd.png) e
e  .
.Como os intervalos vão até o menos infinito, não incluindo o menos infinito e até mais infinito, não incluindo o infinito, eu posso dizer que
![A \cup B= ]-\infty;\infty[ A \cup B= ]-\infty;\infty[](/latexrender/pictures/3c0a8a05ac4bee06f4d891d5404eeb3a.png) ?
?
![A= ]-\infty;8] A= ]-\infty;8]](/latexrender/pictures/c6361ee25c15154ca65b2dc703e7c2cd.png) e
e  .
.![A \cup B= ]-\infty;\infty[ A \cup B= ]-\infty;\infty[](/latexrender/pictures/3c0a8a05ac4bee06f4d891d5404eeb3a.png) ?
?

![-]8;10[ -]8;10[](/latexrender/pictures/53cbb8e4a6dd03b99d2f7e3ed91ee695.png) , você poderia me explicar?
, você poderia me explicar?
![A= ]-\infty;8[ e B= [10;\infty[. A= ]-\infty;8[ e B= [10;\infty[.](/latexrender/pictures/01c2940850028aa6d3594f07c1bdc8ec.png)
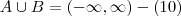 ?
?
 e
e  voce verá que há um "rombo" que é justamente o intervalo
voce verá que há um "rombo" que é justamente o intervalo 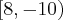 (perceba que o oito não faz parte do conjunto
(perceba que o oito não faz parte do conjunto  ), então se esse intervalo não está contido em nenhum dos dois conjuntos, portanto quando se fizer a união dos dois ele tambem não irá estar incluído logo a resposta será toda a reta exceto esse intervalo:
), então se esse intervalo não está contido em nenhum dos dois conjuntos, portanto quando se fizer a união dos dois ele tambem não irá estar incluído logo a resposta será toda a reta exceto esse intervalo: .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)